7376. В правильной треугольной призме ABCA_{1}B_{1}C_{1}
, все рёбра которой равны, найдите косинус угла между плоскостями ACB_{1}
и BA_{1}C_{1}
.
Ответ. \frac{1}{7}
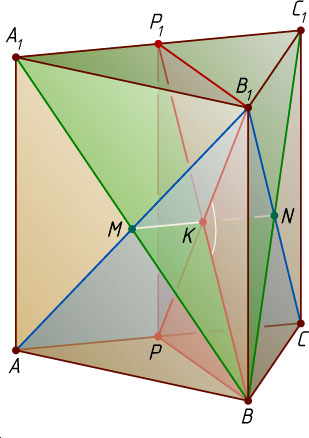
Решение. Пусть все рёбра призмы равны a
, точки P
и P_{1}
— середины рёбер AC
и A_{1}C_{1}
соответственно, M
и N
— центры боковых граней соответственно ABB_{1}A_{1}
и BCC_{1}B_{1}
.
Поскольку M
и N
— общие точки плоскостей ACB_{1}
и BA_{1}C_{1}
, эти плоскости пересекаются по прямой MN
. Пусть прямые B_{1}P
и BP_{1}
, лежащие в плоскости BPP_{1}B_{1}
, пересекаются в точке K
. Тогда B_{1}K
и BK
— медианы, а значит, и высоты равнобедренных треугольников MB_{1}N
и MBN
, причём B_{1}K=BK=\frac{1}{2}BP_{1}
, так как MN
— средняя линия треугольника BA_{1}C_{1}
.
Угол BKB_{1}
— линейный угол одного из двугранных углов, образованных плоскостями ACB_{1}
и BA_{1}C_{1}
. Из прямоугольного треугольника BP_{1}A_{1}
находим, что
BP_{1}=\sqrt{BA_{1}^{2}-A_{1}P_{1}^{2}}=\sqrt{(a\sqrt{2})^{2}-\left(\frac{a}{2}\right)^{2}}=\frac{a\sqrt{7}}{2},
поэтому B_{1}K=BK=\frac{1}{2}BP_{1}=\frac{a\sqrt{7}}{4}
.
По теореме косинусов из треугольника BKB_{1}
находим, что
\cos\angle BKB_{1}=\frac{BK^{2}+BK_{1}^{2}-BB_{1}^{2}}{2BK\cdot B_{1}K}=\frac{\frac{7a^{2}}{16}+\frac{7a^{2}}{16}-a^{2}}{2\cdot\frac{a\sqrt{7}}{4}\cdot\frac{a\sqrt{7}}{4}}=-\frac{1}{7}.
Следовательно, косинус угла между плоскостями ACB_{1}
и BA_{1}C_{1}
равен \frac{1}{7}
.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 3.3, с. 7
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4(в), с. 26
