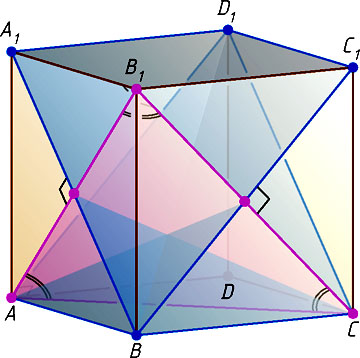
7377. В кубе ABCDA_{1}B_{1}C_{1}D_{1}
найдите угол между плоскостями ABC_{1}
и BCD_{1}
.
Ответ. 60^{\circ}
Указание. Угол между плоскостями равен углу между прямыми, соответственно перпендикулярными этим плоскостям.
Решение. Прямая B_{1}C
перпендикулярна плоскости ABC_{1}D_{1}
, так как эта прямая перпендикулярна двум пересекающимся прямым BC_{1}
и AB
этой плоскости. Аналогично прямая AB_{1}
перпендикулярна плоскости BCD_{1}A_{1}
. Угол между плоскостями равен углу между прямыми, соответственно перпендикулярными этим плоскостям, поэтому искомый угол равен углу AB_{1}C
, а так как треугольник AB_{1}C
равносторонний, то \angle AB_{1}C=60^{\circ}
.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 8, с. 57
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1(г), с. 26
