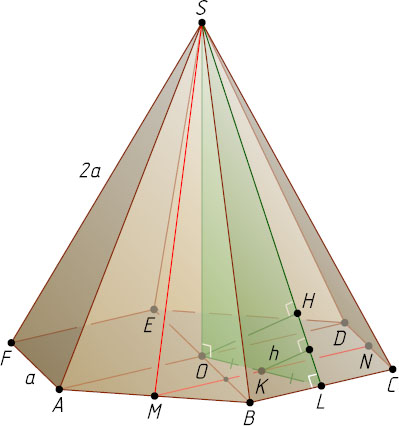
7387. Точка M
— середина стороны AB
основания ABCDEF
правильной шестиугольной пирамиды SABCDEF
. Найдите синус угла между прямой SM
и плоскостью BSC
, если известно, что боковое ребро вдвое больше стороны основания.
Ответ. \frac{1}{5}
.
Решение. Пусть O
— центр правильного шестиугольника ABCDEF
, N
и L
— середины сторон CD
и BC
соответственно, K
— точка пересечения отрезков MN
и OL
.
Прямая MN
параллельна плоскости SBC
, так как эта прямая параллельна прямой BC
плоскости BSC
, значит, расстояние от точки M
до плоскости SBC
равно расстоянию до этой плоскости от любой точки прямой MN
, в частности, от точки K
. Поскольку K
— середина OL
, расстояние от точки K
до плоскости SBC
вдвое меньше расстояния до этой плоскости от точки O
.
Пусть OH
— перпендикуляр, опущенный из точки O
на медиану SL
равнобедренного треугольника BSC
. Прямая OH
перпендикулярна двум пересекающимся прямым SL
и BC
плоскости BSC
, значит, OH
— перпендикуляр к этой плоскости.
Пусть сторона основания пирамиды равна a
. Тогда боковое ребро равно 2a
, OL=\frac{a\sqrt{3}}{2}
. Из прямоугольных треугольников SBL
и SOB
находим, что
SL=\sqrt{SB^{2}-BL^{2}}=\sqrt{4a^{2}-\frac{a^{2}}{4}}=\frac{a\sqrt{15}}{2},
SO=\sqrt{SB^{2}-OB^{2}}=\sqrt{4a^{2}-a^{2}}=a\sqrt{3}.
Записав двумя способами площадь прямоугольного треугольника SOL
, получим равенство \frac{1}{2}SL\cdot OH=\frac{1}{2}OL\cdot SO
, откуда
OH=\frac{OL\cdot SO}{SL}=\frac{\frac{a\sqrt{3}}{2}\cdot a\sqrt{3}}{\frac{a\sqrt{15}}{2}}=\frac{3a}{\sqrt{15}}.
Тогда расстояние h
от точки K
, а значит, и от точки M
до плоскости BSC
равно \frac{3a}{2\sqrt{15}}
.
Пусть искомый угол между прямой SM
и плоскостью BSC
равен \alpha
. Тогда
\sin\alpha=\frac{h}{SM}=\frac{h}{SL}=\frac{\frac{3a}{2\sqrt{15}}}{\frac{a\sqrt{15}}{2}}=\frac{1}{5}.