7392. В правильной четырёхугольной пирамиде SABCD
, все рёбра которой равны, найдите косинус угла между плоскостями SAD
и SBC
.
Ответ. \frac{1}{3}
.
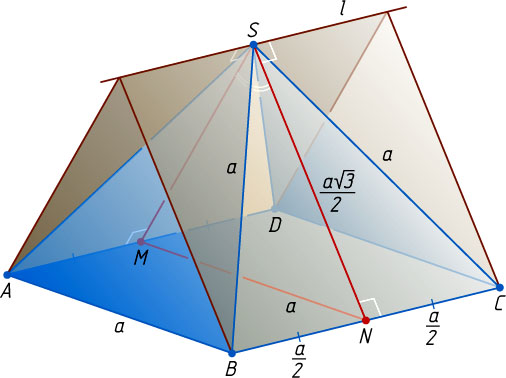
Решение. Пусть все рёбра пирамиды равны a
, M
и N
— середины рёбер AD
и BC
соответственно. Поскольку пересекающиеся плоскости SAD
и SBC
проходят через параллельные прямые AD
и BC
, эти плоскости пересекаются по прямой l
, параллельной прямым AD
и BC
, а так как SM\perp AD
и SN\perp BC
, то SM\perp l
и SN\perp l
. Следовательно, линейный угол двугранного угла, образованного плоскостями SAD
и SBC
, — это угол MSN
.
По теореме косинусов из равнобедренного треугольника MSN
со сторонами SM=SN=\frac{a\sqrt{3}}{2}
и MN=a
находим, что
\cos\angle MSN=\frac{SM^{2}+SN^{2}-MN^{2}}{2SM\cdot SN}=\frac{\frac{3a^{2}}{4}+\frac{3a^{2}}{4}-a^{2}}{2\cdot\frac{a\sqrt{3}}{2}\cdot\frac{a\sqrt{3}}{2}}=\frac{1}{3}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 4, с. 25
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 3(а), с. 26
