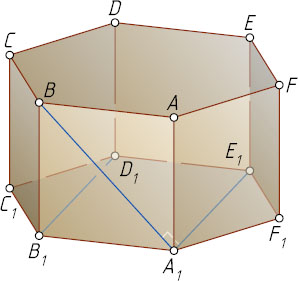
7465. В правильной шестиугольной призме ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}
найдите угол между прямыми BA_{1}
и B_{1}D_{1}
.
Ответ. 90^{\circ}
.
Решение. Поскольку B_{1}D_{1}\parallel A_{1}E_{1}
, угол между скрещивающимися прямыми BA_{1}
и B_{1}D_{1}
равен углу между пересекающимися прямыми BA_{1}
и A_{1}E_{1}
, т. е. углу BA_{1}E_{1}
.
Ортогональная проекция A_{1}B_{1}
наклонной BA_{1}
к плоскости A_{1}B_{1}C_{1}D_{1}E_{1}F_{1}
перпендикулярна прямой A_{1}E_{1}
, лежащей в этой плоскости, значит, BA_{1}\perp A_{1}E_{1}
(теорема о трёх перпендикулярах). Следовательно, \angle BA_{1}E_{1}=90^{\circ}
.