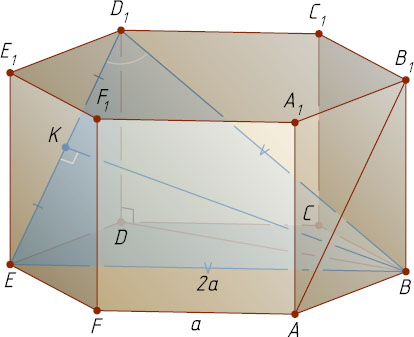
7467. В правильной шестиугольной призме ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}
, все рёбра которой равны, найдите косинус угла между прямыми AB_{1}
и BD_{1}
.
Ответ. \frac{\sqrt{2}}{4}
.
Решение. Поскольку AB_{1}\parallel ED_{1}
, угол между скрещивающимися прямыми AB_{1}
и BD_{1}
равен углу между пересекающимися прямыми ED_{1}
и BD_{1}
, т. е. углу BD_{1}E
.
Пусть сторона основания призмы равна a
. Из прямоугольного треугольника BDD_{1}
находим, что
BD_{1}=\sqrt{DD_{1}^{2}+BD^{2}}=\sqrt{a^{2}+(a\sqrt{3})^{2}}=2a,
а так как BE=2a
, то треугольник D_{1}BE
— равнобедренный с основанием D_{1}E=a\sqrt{2}
. Его медиана BK
является высотой, следовательно,
\cos\angle BD_{1}E=\cos\angle BD_{1}K=\frac{D_{1}K}{BD_{1}}=\frac{\frac{a\sqrt{2}}{2}}{2a}=\frac{\sqrt{2}}{4}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 3, с. 49
