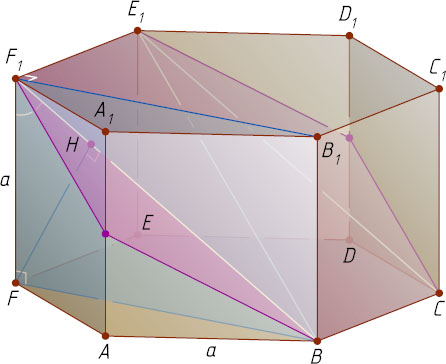
7468. В правильной шестиугольной призме ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}
, все рёбра которой равны, найдите угол между прямой AA_{1}
и плоскостью BCE_{1}
.
Ответ. 60^{\circ}
.
Решение. Поскольку AA_{1}\parallel FF_{1}
, угол между прямой AA_{1}
и плоскостью BCE_{1}
равен углу между прямой FF_{1}
и плоскостью BCE_{1}
.
Пусть все рёбра данной призмы равны a
, H
— основание перпендикуляра, опущенного из точки F
на BF_{1}
. Прямая F_{1}E_{1}
перпендикулярна двум пересекающимся прямым FF_{1}
и B_{1}F_{1}
плоскости BFF_{1}B_{1}
, поэтому F_{1}E_{1}
— перпендикуляр к этой плоскости. Значит, прямая F_{1}E_{1}
перпендикулярна прямой FH
, лежащей в этой плоскости. Таким образом, прямая FH
перпендикулярна двум пересекающимся прямым BF_{1}
и E_{1}F_{1}
плоскости BCE_{1}F_{1}
. Следовательно, FH
— перпендикуляр к этой плоскости, HF_{1}
— ортогональная проекция на эту плоскость наклонной FF_{1}
, а угол FF_{1}H
— угол между прямой FF_{1}
и плоскостью BCE_{1}F_{1}
.
Из прямоугольного треугольника BFF_{1}
находим, что
\tg\angle FF_{1}H=\tg\angle FF_{1}B=\frac{BF}{FF_{1}}=\frac{a\sqrt{3}}{a}=\sqrt{3}.
Следовательно, \angle FF_{1}H=60^{\circ}
.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 7, с. 21
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5(а), с. 45
