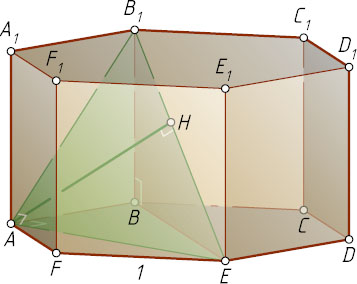
7479. В правильной шестиугольной призме ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}
, все рёбра которой равны 1, найдите расстояние от точки A
до прямой EB_{1}
.
Ответ. \sqrt{\frac{6}{5}}
.
Решение. Расстояние от точки A
до прямой EB_{1}
равно высоте AH
треугольника AEB_{1}
.
Поскольку AB\perp AE
, а AB
— ортогональная проекция наклонной B_{1}A
на плоскость основания ABCDEF
, то по теореме о трёх перпендикулярах B_{1}A\perp AE
. Значит, треугольник AEB_{1}
— прямоугольный, а AH
— его высота, проведённая из вершины прямого угла.
Из прямоугольного треугольника BB_{1}E
находим, что
EB_{1}=\sqrt{BB_{1}^{2}+BE^{2}}=\sqrt{1+4}=\sqrt{5}.
Записав двумя способами площадь треугольника AEB_{1}
, получим равенство \frac{1}{2}EB_{1}\cdot AH=\frac{1}{2}AE\cdot AB_{1}
, откуда
AH=\frac{AE\cdot AB_{1}}{EB_{1}}=\frac{\sqrt{3}\cdot\sqrt{2}}{\sqrt{5}}=\sqrt{\frac{6}{5}}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 11, с. 46
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5(д), с. 35
