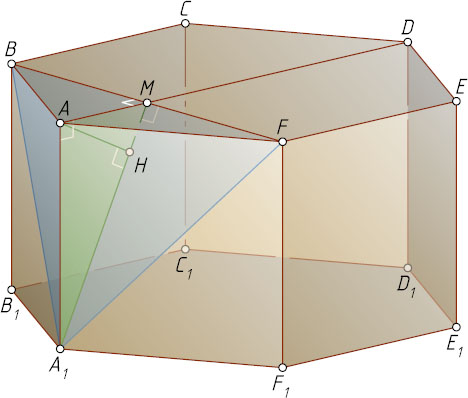
7483. В правильной шестиугольной призме ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}
, все рёбра которой равны 1, найдите расстояние от точки A
до плоскости BFA_{1}
.
Ответ. \frac{1}{\sqrt{5}}
.
Решение. Пусть M
— точка пересечения диагоналей AD
и BF
основания ABCDEF
. Тогда M
— середина BF
, AM\perp BF
, AM=\frac{1}{4}AD=\frac{1}{2}
. Из прямоугольного треугольника AMA_{1}
находим, что
MA_{1}=\sqrt{AM^{2}+AA_{1}^{2}}=\sqrt{\frac{1}{4}+1}=\frac{\sqrt{5}}{2}.
Пусть AH
— высота прямоугольного треугольника AMA_{1}
. Прямая BF
перпендикулярна двум пересекающимся прямым AM
и AA_{1}
плоскости AMA_{1}
, содержащей прямую AH
, значит, AH\perp BF
. Прямая AH
перпендикулярна двум пересекающимся прямым BF
и MA_{1}
плоскости BFA_{1}
, значит, AH
— перпендикуляр к этой плоскости. Следовательно, расстояние от точки A
до плоскости BFA_{1}
равно длине отрезка AH
.
Записав двумя способами площадь прямоугольного треугольника AMA_{1}
, получим равенство \frac{1}{2}MA_{1}\cdot AH=\frac{1}{2}AM\cdot AA_{1}
, откуда
AH=\frac{AM\cdot AA_{1}}{MA_{1}}=\frac{\frac{1}{2}\cdot1}{\frac{\sqrt{5}}{2}}=\frac{1}{\sqrt{5}}.
