7486. В правильной шестиугольной пирамиде SABCDEF
с основанием ABCDEF
найдите косинус угла между прямыми SB
и AD
, если известно, что боковое ребро вдвое больше стороны основания.
Ответ. \frac{1}{4}
.
Решение. Поскольку AD\parallel BC
, угол между скрещивающимися прямыми SB
и AD
равен углу между пересекающимися прямыми SB
и BC
, т. е. углу CBS
.
Пусть сторона основания и боковое ребро данной пирамиды равны a
и 2a
соответственно, M
— середина ребра BC
. Тогда SM
— медиана, а значит, и высота равнобедренного треугольника BSC
, BM=\frac{1}{2}BC=\frac{a}{2}
. Следовательно,
\cos\angle CBS=\cos\angle MBS=\frac{BM}{SB}=\frac{\frac{a}{2}}{2a}=\frac{1}{4}.
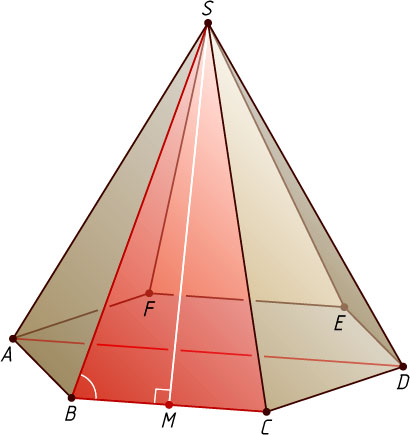
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 8, с. 16
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6(г), с. 17
