7487. В правильной шестиугольной пирамиде SABCDEF
с основанием ABCDEF
найдите косинус угла между плоскостями SBC
и SEF
, если известно, что боковое ребро вдвое больше стороны основания.
Ответ. \frac{3}{5}
.
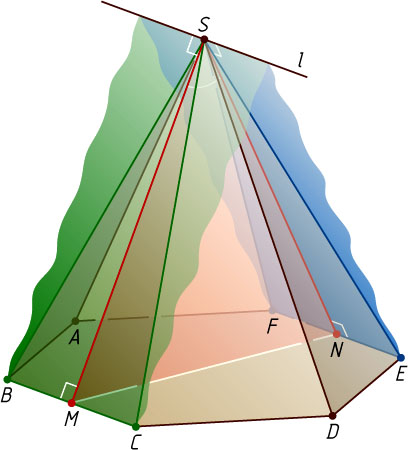
Решение. Первый способ. Пересекающиеся плоскости SBC
и SEF
проходят через параллельные прямые BC
и EF
соответственно, значит, эти плоскости пересекаются по прямой l
, параллельной BC
и EF
. Медианы SM
и SN
боковых граней соответственно SBC
и SEF
являются высотами равнобедренных треугольников, а так как основания BC
и EF
этих треугольников параллельны прямой l
, то SM\perp l
и SN\perp l
. Следовательно, MSN
— линейный угол двугранного угла, образованного плоскостями SBC
и SEF
.
Пусть BC=a
, SB=2a
. В равнобедренном треугольнике MSN
известны стороны
MN=a\sqrt{3},~SN=SM=\sqrt{SB^{2}-MB^{2}}=\sqrt{4a^{2}-\frac{a^{2}}{4}}=\frac{a\sqrt{15}}{2}.
Из этого треугольника по теореме косинусов находим, что
\cos\angle MSN=\frac{SM^{2}+SN^{2}-MN^{2}}{2SM\cdot SN}=\frac{\frac{15a^{2}}{4}+\frac{15a^{2}}{4}-3a^{2}}{2\cdot\frac{a\sqrt{15}}{2}\cdot\frac{a\sqrt{15}}{2}}=\frac{3}{5}.
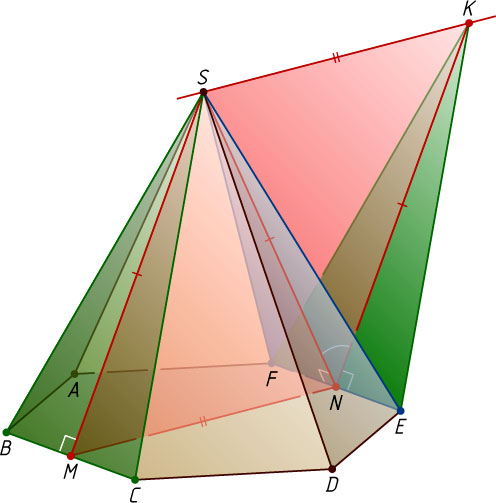
Второй способ. Пусть M
и N
— середины рёбер BC
и EF
соответственно. Через вершину S
проведём прямую, параллельную MN
, и отметим на ней такую точку K
, что SK=MN
и точки K
и M
лежат по разные стороны от плоскости SEF
. Тогда MSKN
— параллелограмм, поэтому KN\parallel SM
и KN=SM
.
Плоскость KFE
параллельна плоскости SBC
, поэтому угол между плоскостями SBC
и SEF
равен углу между плоскостями KFE
и SEF
. Поскольку SN\perp EF
и KN\perp EF
, линейный угол двугранного угла, образованного этими плоскостями, — это угол KNS
.
Пусть BC=a
, SB=2a
. В равнобедренном треугольнике KNS
известны стороны
KS=MN=a\sqrt{3},~KN=SM=SN=\sqrt{SF^{2}-FN^{2}}=\sqrt{4a^{2}-\frac{a^{2}}{4}}=\frac{a\sqrt{15}}{2}.
Из этого треугольника по теореме косинусов находим, что
\cos\angle KNS=\frac{SN^{2}+KN^{2}-KS^{2}}{2SN\cdot KN}=\frac{\frac{15a^{2}}{4}+\frac{15a^{2}}{4}-3a^{2}}{2\cdot\frac{a\sqrt{15}}{2}\cdot\frac{a\sqrt{15}}{2}}=\frac{3}{5}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 6, с. 25
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6(а), с. 26

