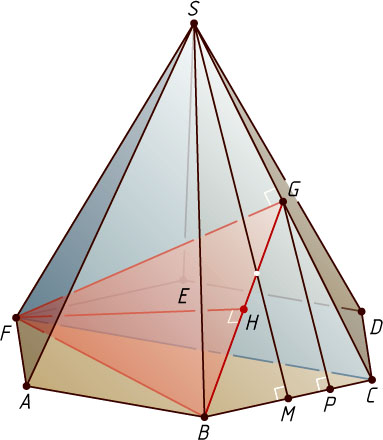
7491. В правильной шестиугольной пирамиде SABCDEF
с основанием ABCDEF
найдите расстояние от точки F
до прямой BG
, где G
— середина ребра SC
, если известно, что стороны основания равны 1, а боковые рёбра равны 2.
Ответ. \frac{\sqrt{42}}{4}
.
Решение. Пусть M
— середина ребра BC
, P
— проекция точки G
на прямую BC
. Тогда P
— середина MC
,
SM=\sqrt{SC^{2}-CM^{2}}=\sqrt{4-\frac{1}{4}}=\frac{\sqrt{15}}{2},
PG=\frac{1}{2}SM=\frac{\sqrt{15}}{4},~CP=\frac{1}{4},~BP=\frac{3}{4},
BG=\sqrt{BP^{2}+PG^{2}}=\sqrt{\frac{9}{16}+\frac{15}{16}}=\sqrt{\frac{3}{2}}.
Из равностороннего треугольника SCF
со стороной 2 находим, что FG=\sqrt{3}
. Из равнобедренного треугольника ABF
находим, что BF=\sqrt{3}
.
Расстояние от точки F
до прямой BG
равно высоте FH
равнобедренного треугольника BFG
:
FH=\sqrt{BF^{2}-BH^{2}}=\sqrt{(\sqrt{3})^{2}-\left(\frac{1}{2}\sqrt{\frac{3}{2}}\right)^{2}}=
=\sqrt{3-\frac{3}{8}}=\sqrt{\frac{21}{8}}=\frac{\sqrt{42}}{4}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 4.3, с. 8
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6(в), с. 35
