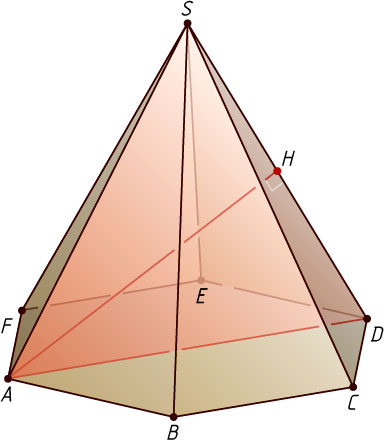
7492. В правильной шестиугольной пирамиде SABCDEF
с основанием ABCDEF
найдите расстояние от точки A
до прямой SD
, если известно, что стороны основания равны 1, а боковые рёбра равны 2.
Ответ. \sqrt{3}
.
Решение. Пусть AH
— медиана равностороннего треугольника ASD
со сторонами SA=SD=AD=2
. Тогда AH
— высота этого треугольника, поэтому расстояние от точки A
до прямой SD
равно длине отрезка AH
, т. е. \sqrt{3}
.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 12, с. 46
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6(г), с. 35
