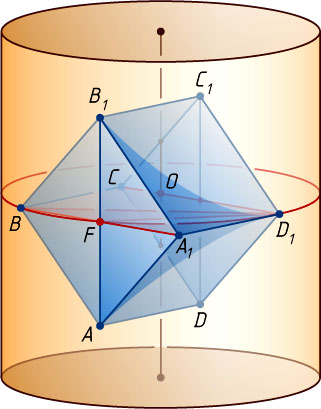
7500. Вершины A
, B
и D_{1}
куба ABCDA_{1}B_{1}C_{1}D_{1}
лежат на боковой поверхности цилиндра, ось которого параллельна прямой DC_{1}
. Найдите радиус основания цилиндра, если ребро куба равно a
.
Ответ. \frac{3a\sqrt{2}}{4}
.
Указание. Рассмотрите ортогональную проекцию цилиндра на плоскость BCD_{1}A_{1}
.
Решение. Рассмотрим ортогональную проекцию цилиндра (рис. 1) на плоскость BCD_{1}A_{1}
(рис. 2). Эта плоскость перпендикулярна прямой DC_{1}
, поэтому она перпендикулярна оси цилиндра. Ортогональные проекции точек B
и D_{1}
на эту плоскость есть сами точки B
и D_{1}
, а ортогональная проекция точки A
— точка F
пересечения диагоналей квадрата ABB_{1}A_{1}
. Ортогональная проекция окружности основания цилиндра — окружность, описанная около треугольника BFD_{1}
. Её радиус r
равен радиусу основания цилиндра.
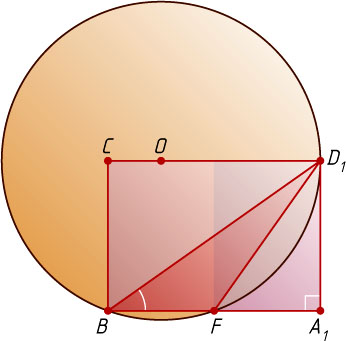
В прямоугольнике BCD_{1}A_{1}
известно, что
A_{1}D_{1}=a,~A_{1}B=a\sqrt{2},~A_{1}F=\frac{a\sqrt{2}}{2},~BD_{1}=a\sqrt{3},
FD_{1}=\sqrt{A_{1}D^{2}+A_{1}F^{2}}=\sqrt{a^{2}+\frac{a^{2}}{2}}=a\sqrt{\frac{3}{2}},
\sin\angle FBD_{1}=\frac{A_{1}D_{1}}{BD_{1}}=\frac{1}{\sqrt{3}}.
Следовательно,
r=\frac{FD_{1}}{2\sin\angle FBD_{1}}=\frac{a\sqrt{\frac{3}{2}}}{\frac{2}{\sqrt{3}}}=\frac{3a\sqrt{2}}{4}.
Источник: Пособие по математике для поступающих в вузы / Под ред. Г. Н. Яковлева. — 3-е изд. — М.: Наука, 1988. — с. 508

