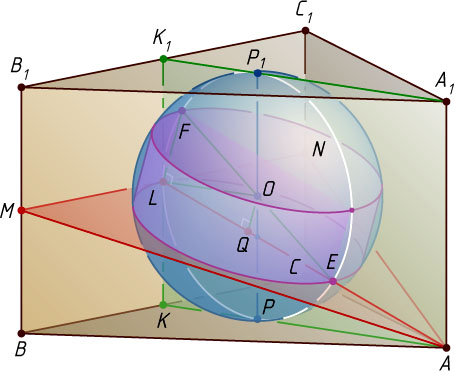
7509. Правильная треугольная призма ABCA_{1}B_{1}C_{1}
описана около шара радиуса R
. Точки M
и N
— середины рёбер BB_{1}
и CC_{1}
. В шар вписан цилиндр так, что его основание лежит в плоскости AMN
. Найдите объём цилиндра.
Ответ. \frac{9\pi R^{3}}{5\sqrt{10}}
.
Решение. Заметим, что высота призмы равна диаметру шара, т. е. 2R
, шар касается плоскостей оснований призмы в центрах P
и P_{1}
равносторонних треугольников ABC
и A_{1}B_{1}C_{1}
, а плоскостей боковых граней — в точках пересечения их диагоналей (рис. 1).
Пусть K
и K_{1}
— середины BC
и B_{1}C_{1}
соответственно. Ортогональная проекция шара на плоскость ABC
есть круг радиуса R
, вписанный в треугольник ABC
. Поэтому
AP=A_{1}P_{1}=2R,~PK=P_{1}K_{1}=R,~AK=A_{1}K_{1}=3R.
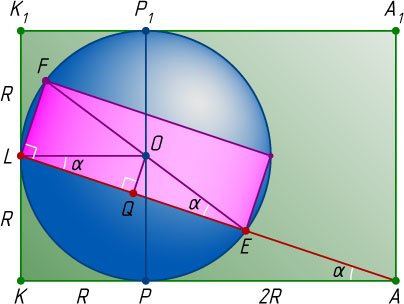
Рассмотрим сечение призмы плоскостью AKK_{1}A_{1}
(рис. 2). Получим прямоугольник AKK_{1}A_{1}
со сторонами 2R
, 3R
, круг радиуса R
, касающийся сторон AK
и A_{1}K_{1}
в точках P
и P_{1}
, а стороны KK_{1}
— в её середине L
, причём центр круга совпадает с центром O
шара. Пусть \angle LAK=\alpha
. Тогда
\tg\alpha=\frac{KL}{AK}=\frac{R}{3R}=\frac{1}{3},~\cos\alpha=\frac{3}{\sqrt{10}}.
Опустим перпендикуляр OQ
из центра круга на прямую AL
. Из прямоугольного треугольника OQL
находим, что
QL=OL\cos\angle OLQ=R\cos\alpha=\frac{3R}{\sqrt{10}}.
Пусть AQ
пересекает окружность, ограничивающую круг, в точке E
. Продолжим EO
до пересечения с этой окружностью в точке F
. Тогда EL
— диаметр основания цилиндра, вписанного в данный шар, а LF
— высота цилиндра. По теореме Пифагора из прямоугольного треугольника EFL
находим, что
LF=\sqrt{EF^{2}-EL^{2}}=\sqrt{4R^{2}-\left(\frac{6R}{\sqrt{10}}\right)^{2}}=\frac{2R}{\sqrt{10}}.
Следовательно, объём цилиндра равен
\pi\cdot QL^{2}\cdot LF=\pi\left(\frac{3R}{\sqrt{10}}\right)^{2}\cdot\frac{2R}{\sqrt{10}}=\frac{9\pi R^{3}}{5\sqrt{10}}.