7630. Плоские углы при вершине правильной треугольной пирамиды равны \alpha
. Найдите двугранные углы при основании пирамиды.
Ответ. \arccos\frac{\tg\frac{\alpha}{2}}{\sqrt{3}}
.
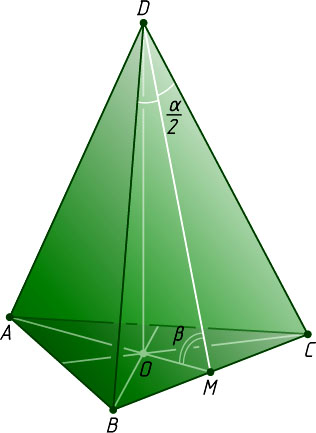
Решение. Пусть O
— центр основания ABC
правильной треугольной пирамиды ABCD
, M
— середина BC
, \angle BDC=\angle ADB=\angle ADC=\alpha
. Обозначим AB=BC=AC=a
, \angle OMD=\beta
.
Так как DM\perp BC
и OM\perp BC
, то OMD
— линейный угол двугранного угла пирамиды при ребре BC
, \angle OMD=\beta
. Тогда
DM=BM\ctg\angle BDM=\frac{a}{2}\ctg\alpha,
\cos\beta=\cos\angle OMD=\frac{OM}{DM}=\frac{\frac{a\sqrt{3}}{6}}{\frac{a}{2}\ctg\alpha}=\frac{\tg\alpha}{\sqrt{3}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 19(а), с. 68
