7674. В кубе ABCDA_{1}B_{1}C_{1}D_{1}
найдите тангенс угла между плоскостями ABC
и DA_{1}C_{1}
.
Ответ. \sqrt{2}
.
Решение. Плоскость ABCD
параллельна плоскости A_{1}B_{1}C_{1}D_{1}
, поэтому угол между плоскостями ABCD
и DA_{1}C_{1}
равен углу между плоскостями A_{1}B_{1}C_{1}D_{1}
и DA_{1}C_{1}
.
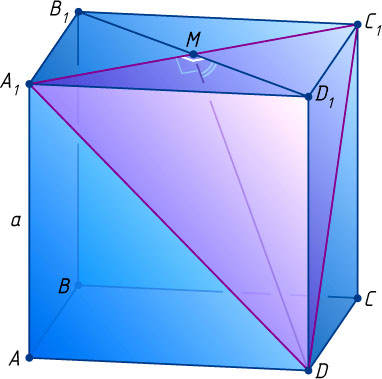
Пусть M
— точка пересечения диагоналей квадрата A_{1}B_{1}C_{1}D_{1}
. Тогда D_{1}M\perp A_{1}C_{1}
и DM\perp A_{1}C_{1}
(как медиана равнобедренного треугольника DA_{1}C_{1}
). Следовательно, линейный угол двугранного угла, образованного плоскостями A_{1}B_{1}C_{1}D_{1}
и DA_{1}C_{1}
, — это угол DMD_{1}
.
Пусть ребро куба равно a
. Тогда D_{1}M=\frac{a\sqrt{2}}{2}
и DD_{1}=a
. Из прямоугольного треугольника DD_{1}M
находим, что
\tg\angle DMD_{1}=\frac{DD_{1}}{D_{1}M}=\frac{a}{\frac{a\sqrt{2}}{2}}=\sqrt{2}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 9, с. 51
