7680. В единичном кубе ABCDA_{1}B_{1}C_{1}D_{1}
найдите расстояние между прямыми BA_{1}
и DB_{1}
.
Ответ. \frac{\sqrt{6}}{6}
.
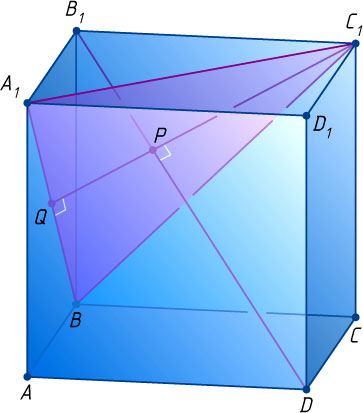
Решение. Известно, что диагональ DB_{1}
куба ABCDA_{1}B_{1}C_{1}D_{1}
перпендикулярна плоскости BA_{1}C_{1}
, содержащей прямую A_{1}B
, и проходит через центр P
равностороннего треугольника BA_{1}C_{1}
. Высота C_{1}Q
этого треугольника проходит через точку Q
и делится ею в отношении 2:1
, считая от точки C_{1}
. Поскольку PQ\perp DB_{1}
и PQ\perp BA_{1}
, отрезок PQ
— общий перпендикуляр скрещивающихся прямых BA_{1}
и DB_{1}
, а так как C_{1}P:PQ=2:1
, то
PQ=\frac{1}{3}C_{1}Q=\frac{1}{3}\cdot\frac{BA_{1}\sqrt{3}}{2}=\frac{1}{3}\cdot\sqrt{2}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{6}}{6}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 1, с. 40
