7696. В правильной четырёхугольной пирамиде SABCD
, все рёбра которой равны 1, найдите синус угла между плоскостью SAD
и плоскостью, проходящей через точку A
перпендикулярно прямой BD
.
Ответ. \sqrt{\frac{2}{3}}
.
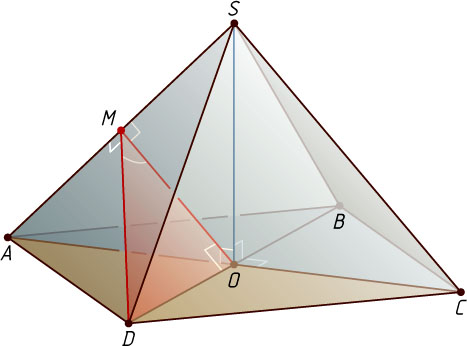
Решение. Пусть O
— центр основания пирамиды, M
— середина ребра SA
. Прямая BD
перпендикулярна двум пересекающимся прямым AC
и SO
плоскости ASC
, значит, прямая BD
перпендикулярна этой плоскости. Следовательно, плоскость, проходящая через точку A
перпендикулярно прямой BD
, — это плоскость ASC
.
Из прямоугольного треугольника ASO
находим, что
SO=\sqrt{SA^{2}-OA^{2}}=\sqrt{1-\frac{1}{2}}=\frac{\sqrt{2}}{2}=OA.
Медиана OM
равнобедренного треугольника ASO
перпендикулярна стороне SA
. Медиана DM
равностороннего треугольника ASD
также перпендикулярна стороне SA
. Следовательно, линейный угол, образованный плоскостями SAD
и ASC
, — это угол DMO
.
Прямая BD
перпендикулярна плоскости ASC
, поэтому DO\perp OM
, значит, треугольник DMO
— прямоугольный. Следовательно,
\sin\angle DMO=\frac{OD}{DM}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}=\sqrt{\frac{2}{3}}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2011, задача C2
