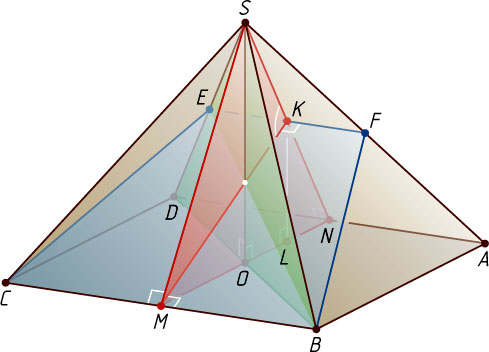
7698. В правильной четырёхугольной пирамиде SABCD
, все рёбра которой равны 1, найдите косинус угла между плоскостями SAD
и BCF
, где F
— середина ребра AS
.
Ответ. \frac{1}{\sqrt{33}}
.
Решение. Плоскость BCF
проходит через прямую BC
, параллельную плоскости SAD
, и пересекает эту плоскость, поэтому прямая пересечения параллельна прямой BC
, а значит, и прямой AD
. Следовательно, если E
— точка пересечения плоскости BCF
с ребром SD
, то FE
— средняя линия треугольника SAD
, а BFEC
— равнобедренная трапеция.
Пусть O
— центр основания пирамиды, M
и N
— середины рёбер BC
и AD
соответственно. Тогда точка K
пересечения SN
и FE
— середина FE
. Из прямоугольного треугольника DSO
находим, что
SO=\sqrt{SD^{2}-OD^{2}}=\sqrt{1-\frac{1}{2}}=\frac{\sqrt{2}}{2}.
Отрезок KM
— высота равнобедренной трапеции BFEC
, поэтому KM\perp FE
, а так как FE\parallel AD
, то KS\perp FE
, значит, линейный угол одного из двугранных углов, образованных плоскостями SAD
и BCF
— это угол MKS
.
Пусть L
— ортогональная проекция точки K
на плоскость основания пирамиды. Тогда L
— середина ON
, KL
— средняя линия прямоугольного треугольника SON
, поэтому
KL=\frac{1}{2}SO=\frac{\sqrt{2}}{4},~KM=\sqrt{KL^{2}+ML^{2}}=\sqrt{\left(\frac{\sqrt{2}}{4}\right)^{2}+\left(\frac{3}{4}\right)^{2}}=\frac{\sqrt{11}}{4},
а так как SN
— высота равностороннего треугольника SAD
, то SN=SM=\frac{\sqrt{3}}{2}
, а KS=\frac{1}{2}SN=\frac{\sqrt{3}}{4}
.
По теореме косинусов из треугольника SKM
находим, что
\cos\angle MKS=\frac{KM^{2}+KS^{2}-SM^{2}}{2KM\cdot KS}=\frac{\frac{11}{16}+\frac{3}{16}-\frac{3}{4}}{2\cdot\frac{\sqrt{11}}{4}\cdot\frac{\sqrt{3}}{4}}=\frac{1}{\sqrt{33}}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2011, задача C2
