7699. В правильной четырёхугольной пирамиде SABCD
, все рёбра которой равны 1, найдите косинус угла между плоскостями ABG
и CDF
, где F
— середина ребра SB
, G
— середина ребра SC
.
Ответ. \frac{7}{11}
.
Решение. Первый способ. Плоскость ABG
проходит через прямую AB
, параллельную плоскости SCD
, и пересекает эту плоскость, поэтому прямая пересечения параллельна прямой AB
, а значит, и прямой CD
. Следовательно, если G_{1}
— точка пересечения плоскости ABG
с ребром SD
, то GG_{1}
— средняя линия треугольника SCD
, а ABGG_{1}
— равнобедренная трапеция. Аналогично, если F_{1}
— точка пересечения плоскости CDF
с ребром SA
, то DCFF_{1}
— также равнобедренная трапеция.
Пусть P
— точка пересечения медиан BG
и CF
треугольника SBC
, а Q
— точка пересечения медиан AG_{1}
и DF_{1}
треугольника SAD
. Тогда плоскости ABG
и CDF
пересекаются по прямой PQ
, а так как BP:PG=CP:PF=DQ:QF_{1}=AQ:QG_{1}=2
, то прямая PQ
параллельна основаниям обеих трапеций.
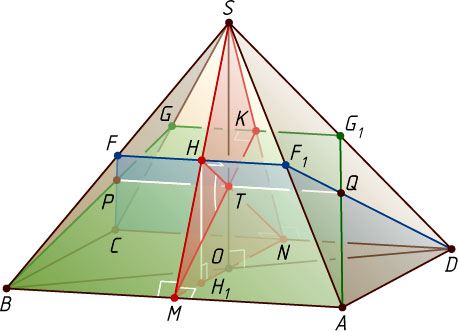
Пусть K
— точка пересечения средней линии GG_{1}
треугольника SCD
с его медианой SN
, а H
— точка пересечения средней линии FF_{1}
треугольника SAB
с его медианой SM
. Тогда K
и H
— середины GG_{1}
и FF_{1}
, а MK
и NH
— высоты равнобедренных трапеций ABGG_{1}
и DCFF_{1}
и, кроме того, — медианы равнобедренного треугольника SMN
. Точка T
пересечения этих медиан лежит на отрезке PQ
, так как MT:TK=BP:PG=2
. При этом TH\perp PQ
и TM\perp PQ
, следовательно, линейный угол одного из двугранных углов, образованных плоскостями ABG
и CDF
, — это угол MTH
.
Пусть O
— центр основания пирамиды. Из прямоугольного треугольника DSO
находим, что
SO=\sqrt{SD^{2}-OD^{2}}=\sqrt{1-\frac{1}{2}}=\frac{\sqrt{2}}{2}.
Пусть H_{1}
— ортогональная проекция точки H
на плоскость основания пирамиды. Тогда H_{1}
— середина OM
, HH_{1}
— средняя линия прямоугольного треугольника SOM
, поэтому
HH_{1}=\frac{1}{2}SO=\frac{\sqrt{2}}{4},~NH=\sqrt{HH_{1}^{2}+NH_{1}^{2}}=
=\sqrt{\left(\frac{\sqrt{2}}{4}\right)^{2}+\left(\frac{3}{4}\right)^{2}}=\frac{\sqrt{11}}{4},
TH=\frac{1}{3}NH=\frac{\sqrt{11}}{12},~TM=TN=\frac{2}{3}NH=\frac{\sqrt{11}}{6},
а так как SM
— высота равностороннего треугольника SAB
, то SM=\frac{\sqrt{3}}{2}
, а MH=\frac{1}{2}SM=\frac{\sqrt{3}}{4}
.
По теореме косинусов из треугольника MTH
находим, что
\cos\angle MTH=\frac{TH^{2}+TM^{2}-MH^{2}}{2NH\cdot NM}=\frac{\frac{11}{144}+\frac{11}{36}-\frac{3}{16}}{2\cdot\frac{\sqrt{11}}{12}\cdot\frac{\sqrt{11}}{6}}=\frac{7}{11}.
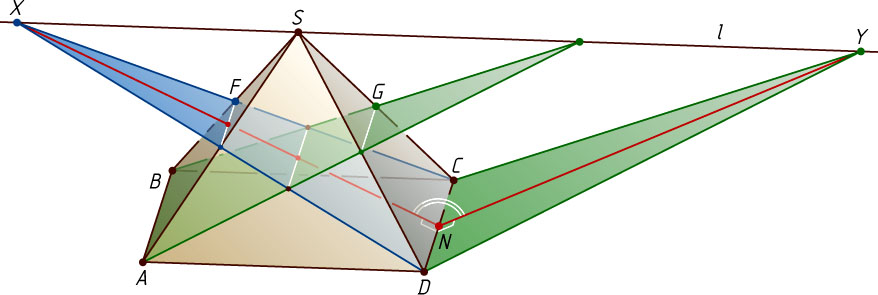
Второй способ. Пересекающиеся плоскости SBC
и SAD
проходят через параллельные прямые BC
и AD
, значит, прямая l
их пересечения проходит через точку S
и параллельна BC
и AD
.
Пусть прямые CF
и l
, лежащие в плоскости SBC
, пересекаются в точке X
, а прямая, проходящая через точку C
параллельно BG
, пересекается с прямой l
в точке Y
. Тогда по признаку параллельности плоскостей плоскость CDY
параллельна плоскости ABG
. Следовательно, угол между плоскостями ABG
и CDF
равен углу между плоскостями CDY
и CDX
. При этом
SX=BC=1,~SY=2BC=2,~XY=SX+SY=3,~CX=2CF=2\cdot\frac{\sqrt{3}}{2}=\sqrt{3}.
Медианы XN
и YN
равнобедренных треугольников CDX
и CDY
перпендикулярны прямой CD
пересечения плоскостей CDX
и CDY
, значит, линейный угол одного из двугранных углов, образованного этими плоскостями, — это угол XNY
.
В треугольнике XNY
известно, что
XY=3,~YN=XN=\sqrt{CX^{2}-CN^{2}}=\sqrt{3-\frac{1}{4}}=\frac{\sqrt{11}}{4}.
По теореме косинусов
\cos\angle XNY=\frac{XN^{2}+YN^{2}-XY^{2}}{2XN\cdot YN}=\frac{\frac{11}{4}+\frac{11}{4}-9}{2\cdot\frac{\sqrt{11}}{2}\cdot\frac{\sqrt{11}}{2}}=-\frac{7}{11},
а так как угол между плоскостями не может быть тупым, то косинус угла между плоскостями ABG
и CDF
равен \frac{7}{11}
.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2011, задача C2

