7968. В шаре радиуса \sqrt{3}
просверлено цилиндрическое отверстие; ось цилиндра проходит через центр шара, а диаметр основания цилиндра равен радиусу шара. Найдите объём оставшейся части шара.
Ответ. \frac{9\pi}{2}
.
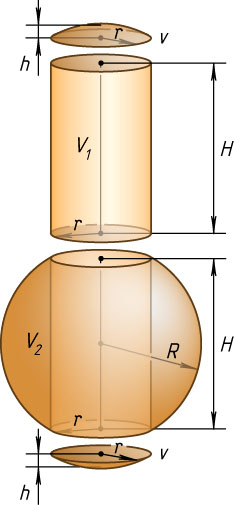
Решение. Пусть R=\sqrt{3}
— радиус шара, r
— радиус отверстия, H
— высота цилиндрической части отверстия, h
— высота каждого из двух шаровых сегментов, которые вместе с цилиндрической частью составляют высверленную часть шара, V
— объём шара, V_{1}
— объём цилиндрической части отверстия, v
— объём каждого из указанных сегментов, V_{2}
— объём оставшейся после высверливания части шара. Тогда
r=\frac{R}{2},~H=\sqrt{(2R)^{2}-R^{2}}=R\sqrt{3},
h=\frac{2R-H}{2}=\frac{2R-R\sqrt{3}}{2}=\frac{R(2-\sqrt{3})}{2},
V=\frac{4}{3}\pi R^{3},~V_{1}=\pi r^{2}H=\pi\left(\frac{R}{2}\right)^{2}\cdot R\sqrt{3}=\frac{\pi R^{3}\sqrt{3}}{4},
v=\pi h^{2}\left(R-\frac{h}{3}\right)=\pi\left(\frac{R(2-\sqrt{3})}{2}\right)^{2}\cdot\left(R-\frac{R(2-\sqrt{3})}{6}\right)=
=\pi R^{3}(2-\sqrt{3})^{2}\cdot\frac{4+\sqrt{3}}{24}=\frac{\pi R^{3}(7-4\sqrt{3})\cdot(4+\sqrt{3})}{24}=
=\frac{\pi R^{3}(16-9\sqrt{3})}{24},
V_{2}=V-V_{1}-2v=\frac{4}{3}\pi R^{3}-\frac{\pi R^{3}\sqrt{3}}{4}-\frac{\pi R^{3}(16-9\sqrt{3})}{12}=
=\pi R^{3}\left(\frac{4}{3}-\frac{\sqrt{3}}{4}-\frac{16-9\sqrt{3}}{12}\right)=\frac{\pi R^{3}\cdot6\sqrt{3}}{12}=\pi R^{3}\cdot\frac{\sqrt{3}}{2}=
=\pi(\sqrt{3})^{3}\cdot\frac{\sqrt{3}}{2}=\pi\cdot3\sqrt{3}\cdot\frac{\sqrt{3}}{2}=\frac{9\pi}{2}.
Источник: Вступительный экзамен в МЭСИ. —
