8065. В цилиндр с радиусом основания, равным 1, и высотой \frac{12}{3+2\sqrt{3}}
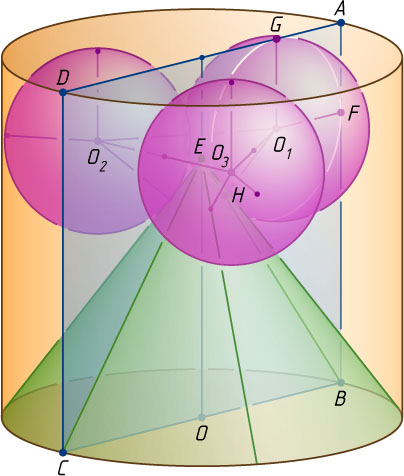
, вписаны три одинаковых шара так, что шары касаются верхнего основания цилиндра, его боковой поверхности и попарно друг друга. Найдите объём конуса, основание которого совпадает с нижним основанием цилиндра и который касается всех трёх шаров.
Ответ. \frac{4}{9}\pi
.
Указание. Рассмотрите: 1) ортогональную проекцию шаров на плоскость основания цилиндра; 2) осевое сечение цилиндра, проходящее через центр одного из шаров.
Решение. Заметим, что
\frac{12}{3+2\sqrt{3}}=\frac{12(2\sqrt{3}-3)}{12-9}=4(2\sqrt{3}-3)=8\sqrt{3}-12.
Пусть O'_{1}
, O'_{2}
, O'_{3}
— ортогональные проекции центров O_{1}
, O_{2}
, O_{3}
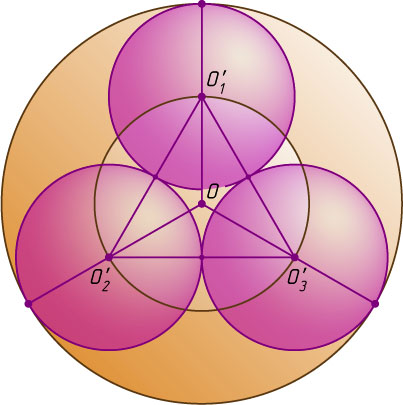
шаров на плоскость нижнего основания цилиндра (рис. 2), O
— центр этого основания, r
— радиус шаров, V
— искомый объём конуса. Точка O
— центр окружности, описанной около равностороннего треугольника O'_{1}O'_{2}O'_{3}
стороной 2r
, поэтому OO'_{1}=\frac{2r}{\sqrt{3}}
, а так как радиус основания цилиндра равен 1, то \frac{2r}{\sqrt{3}}+r=1
, откуда
r=\frac{\sqrt{3}}{2+\sqrt{3}}=\sqrt{3}(2-\sqrt{3})=2\sqrt{3}-3.
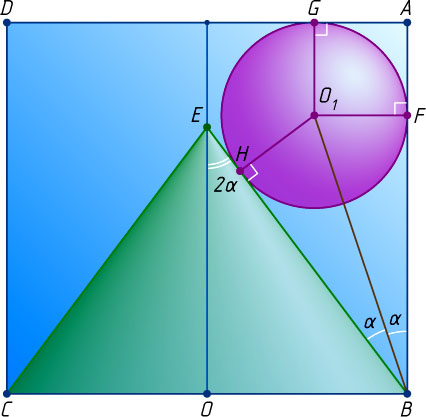
Рассмотрим осевое сечение цилиндра, проходящее через точку O_{1}
(рис. 3). Получим прямоугольник ABCD
, равнобедренный треугольник BCE
с основанием BC=2
и высотой EO
(E
— вершина конуса) и окружность с центром O_{1}
и радиусом r=2\sqrt{3}-3
, касающуюся AB
, AD
и BE
в точках F
, G
и H
соответственно. Обозначим \angle O_{1}BF=\alpha
. Тогда
\tg\alpha=\frac{O_{1}F}{BF}=\frac{O_{1}F}{AB-AF}=\frac{r}{AB-r}=
=\frac{2\sqrt{3}-3}{8\sqrt{3}-12-2\sqrt{3}+3}=\frac{2\sqrt{3}-3}{6\sqrt{3}-9}=\frac{1}{3},
\angle BEO=\angle ABE=2\cdot\angle O_{1}BF=2\alpha,
\tg\angle BEO=\tg2\alpha=\frac{2\tg\alpha}{1-\tg^{2}\alpha}=\frac{2\cdot\frac{1}{3}}{1-\frac{1}{9}}=\frac{3}{4},
OE=\frac{BO}{\tg\angle BEO}=\frac{1}{\tg2\alpha}=\frac{4}{3}.
Следовательно,
V=\frac{1}{3}\pi\cdot OB^{2}\cdot OE=\frac{4}{9}\pi.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1974 (отделение геофизики), вариант 1, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 140


