8191. Ортогональной проекцией равнобедренного прямоугольного треугольника на плоскость \alpha
является правильный треугольник. Найдите угол, образованный гипотенузой данного треугольника с плоскостью \alpha
.
Ответ. \arccos\frac{1}{\sqrt{3}}
.
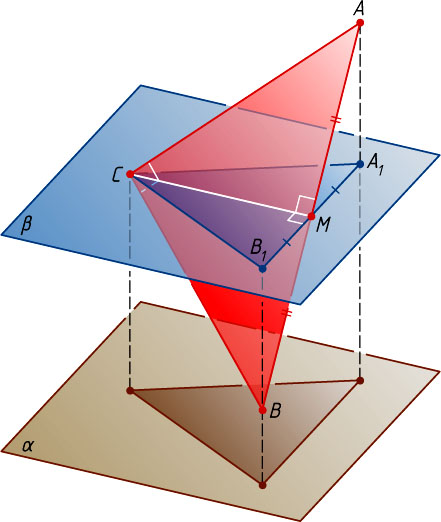
Решение. Пусть C
— вершина прямого угла равнобедренного прямоугольного треугольника ABC
с катетами AC=BC=a
и гипотенузой AB=a\sqrt{2}
; A_{1}
, B_{1}
и C_{1}
— ортогональные проекции точек A
, B
и C
соответственно на плоскость \beta
, параллельную \alpha
и проходящую через вершину C
треугольника ABC
. Обозначим AB=AC=BC=x
.
Прямоугольные треугольники AA_{1}C
и BB_{1}C
равны по гипотенузе и катету. Поэтому AA_{1}=BB_{1}
. Если точки A
и B
лежат по одну сторону от плоскости \beta
, то AA_{1}B_{1}B
— прямоугольник. Поэтому A_{1}B_{1}=AB
. Тогда
C_{1}B_{1}=CB_{1}=A_{1}B_{1}=a\sqrt{2}\gt a=BC,
что невозможно.
Если же точки A
и B
лежат по разные стороны от плоскости \beta
, то отрезок AB
пересекает плоскость \beta
в некоторой точке M
, лежащей на отрезке A_{1}B_{1}
. Из равенства прямоугольных треугольников AA_{1}M
и BB_{1}M
(по катету и противолежащему острому углу) следует, что M
— середина AB
и A_{1}B_{1}
. Поэтому CM
— высота равнобедренного треугольника ABC
и равностороннего треугольника CA_{1}B_{1}
. Значит,
CM=\frac{a\sqrt{2}}{2},~CM=\frac{x\sqrt{3}}{2},
откуда \frac{x}{a}=\frac{\sqrt{2}}{\sqrt{3}}
.
Так как A_{1}M
— ортогональная проекция наклонной AM
на плоскость \beta
, то AMA_{1}
— угол прямой AM
(а значит, и прямой AB
) с плоскостью \beta
. Из прямоугольного треугольника AMA_{1}
находим, что
\cos\angle AMA_{1}=\frac{MA_{1}}{AM}=\frac{\frac{x}{2}}{\frac{a\sqrt{2}}{2}}=\frac{\frac{x}{a}}{\sqrt{2}}=\frac{\frac{\sqrt{2}}{\sqrt{3}}}{\sqrt{2}}=\frac{1}{\sqrt{3}}.
Поскольку плоскости \alpha
и \beta
параллельны, найденный угол равен искомому.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 6, с. 34
