8192. В одной из граней двугранного угла, равного \varphi
, взята точка A
на расстоянии a
от ребра. Найдите расстояние от точки A
до плоскости другой грани.
Ответ. a\sin\varphi
.
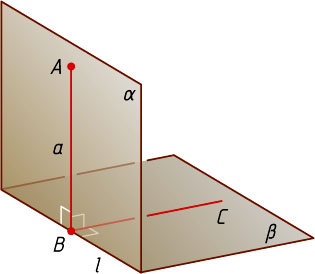
Решение. Пусть \varphi=90^{\circ}
(рис. 1). Через точку A
, лежащую в грани \alpha
данного двугранного угла, проведём прямую, перпендикулярную ребру l
двугранного угла. Пусть проведённая прямая пересекает ребро l
в точке B
. В плоскости \beta
другой грани двугранного угла проведём прямую BC
, перпендикулярную l
. Тогда ABC
— линейный угол данного двугранного угла. В рассматриваемом случае \angle ABC=90^{\circ}
, поэтому прямая AB
перпендикулярна двум пересекающимся прямым l
и BC
плоскости \beta
. Значит, AB
— перпендикуляр к этой плоскости. Тогда расстояние от точки A
до плоскости \beta
равно a
.
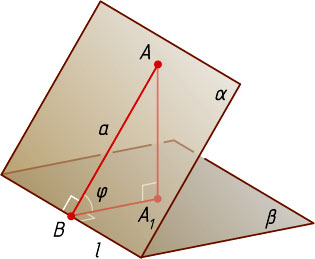
Пусть \varphi\lt90^{\circ}
(рис. 2); A_{1}
— ортогональная проекция точки A
, лежащей в грани \alpha
данного двугранного угла, на плоскость второй его грани \beta
; B
— основание перпендикуляра, опущенного из точки A
на ребро l
данного двугранного угла. По теореме о трёх перпендикулярах A_{1}B\perp l
, поэтому ABA_{1}
— линейный угол данного двугранного угла. По условию задачи \angle ABA_{1}=\varphi
. Расстояние от точки A
до плоскости \beta
равно длине отрезка AA_{1}
. Из прямоугольного треугольника ABA_{1}
находим, что
AA_{1}=AB\sin\angle ABA_{1}=a\sin\varphi.
Если \varphi\gt90^{\circ}
, то аналогично получим, что
AA_{1}=AB\cdot\sin(180^{\circ}-\varphi)=a\sin\varphi.
Эта формула верна и в случае, когда \varphi=90^{\circ}
: AA_{1}=a\sin90^{\circ}=a
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 1, с. 39

