8194. Пусть A
— некоторая точка в пространстве, A_{1}
— проекция точки A
на плоскость \alpha
, AA_{1}=a
. Через точку A
проходит плоскость, образующая угол \varphi
с плоскостью \alpha
и пересекающая плоскость \alpha
по прямой l
. Найдите расстояние от точки A_{1}
до прямой l
.
Ответ. a\ctg\varphi
.
Решение. Если \varphi=90^{\circ}
, то прямая l
проходит через точку A_{1}
. В этом случае искомое расстояние равно 0.
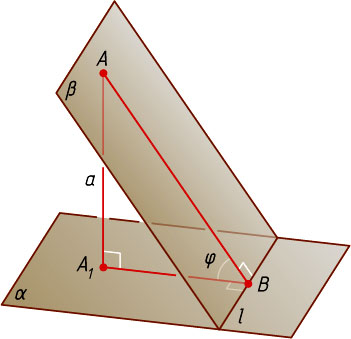
Пусть плоскость \beta
, проходящая через данную точку A
, образует с плоскостью \alpha
угол \varphi\neq90^{\circ}
. Опустим перпендикуляр A_{1}B
из точки A_{1}
на прямую l
. Тогда расстояние от точки A_{1}
до прямой l
равно длине отрезка A_{1}B
. По теореме о трёх перпендикулярах AB\perp l
. Значит, ABA_{1}
— линейный угол двугранного угла, образованного плоскостями \alpha
и \beta
. По условию задачи \angle ABA_{1}=\varphi
. Из прямоугольного треугольника ABA_{1}
находим, что
A_{1}B=AA_{1}\cdot\ctg\angle ABA_{1}=a\ctg\varphi.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 3, с. 39
