8198. Угол между плоскостями равен \alpha
. Найдите площадь ортогональной проекции правильного шестиугольника со стороной 1, лежащего в одной из плоскостей, на другую плоскость.
Ответ. \frac{3\sqrt{3}\cos\alpha}{2}
.
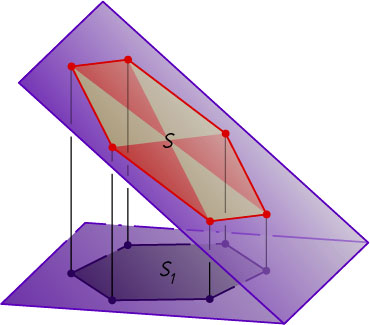
Решение. Пусть S
— площадь данного правильного шестиугольника, лежащего в одной из данных плоскостей, S_{1}
— площадь его ортогональной проекции на другую плоскость. Так как правильный шестиугольник со стороной a
, разбивается большими диагоналями на 6 правильных треугольников со стороной a
, то
S=6\cdot\frac{a^{2}\sqrt{3}}{4}=6\cdot\frac{\sqrt{3}}{4}=\frac{3\sqrt{3}}{2}.
Следовательно,
S_{1}=S\cos\alpha=\frac{3\sqrt{3}}{2}\cdot\cos\alpha.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 7, с. 39
