8200. Через стороны равностороннего треугольника проведены три плоскости, образующие угол \alpha
с плоскостью этого треугольника и пересекающиеся в точке, удалённой на расстояние d
от плоскости треугольника. Найдите радиус окружности, вписанной в данный равносторонний треугольник.
Ответ. d\ctg\alpha
или \frac{1}{3}d\ctg\alpha
.
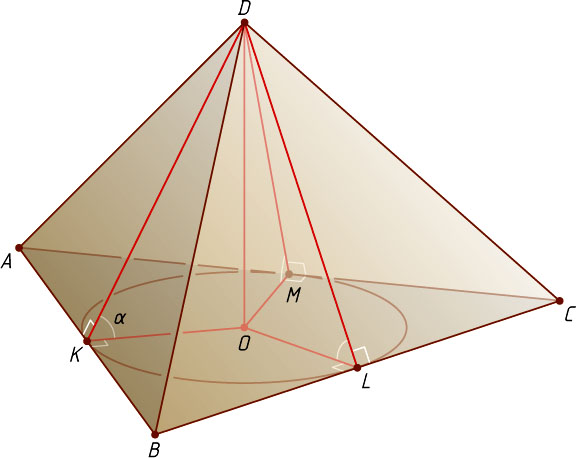
Решение. Пусть плоскости, проходящие через стороны AB
, BC
и AC
равностороннего треугольника ABC
со стороной a
, пересекаются в точке D
и образуют с плоскостью ABC
углы \alpha
. Пусть O
— ортогональная проекция точки D
на плоскость ABC
.
Опустим перпендикуляры OK
, OL
и OM
из точки O
на прямые AB
, BC
и AC
соответственно. По теореме о трёх перпендикулярах DK\perp AB
, DL\perp BC
и DM\perp AC
. Значит, DKO
, DLO
и DMO
— линейные углы двугранных углов, образованных данными плоскостями с плоскостью ABC
. По условию задачи \angle DKO=\angle DLO=\angle DMO=\alpha
. Из равенства прямоугольных треугольников DKO
, DLO
и DMO
(по катету и противолежащему острому углу) следует равенство отрезков OK
, OL
и OM
. Поэтому точка O
равноудалена от прямых AB
, BC
и AC
. Значит, O
— центр вписанной или вневписанной окружности треугольника ABC
.
Пусть O
— центр вписанной окружности равностороннего треугольника ABC
, r
— радиус окружности. Тогда
r=OK=DO\ctg\angle DKO=d\ctg\alpha.
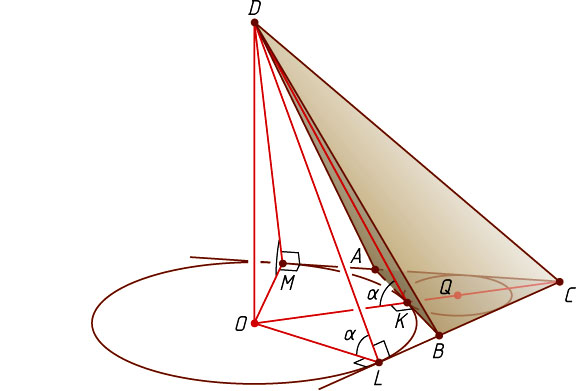
Пусть O
— центр вневписанной окружности треугольника ABC
, касающейся стороны AB
, P
— точка касания этой окружности с продолжением стороны AC
за точку A
, M
— центр вписанной окружности треугольника ABC
. Тогда
OC=\frac{CP}{\cos\angle OCP}=\frac{AC+AP}{\cos30^{\circ}}=\frac{AC+AK}{\cos30^{\circ}}=\frac{a+\frac{a}{2}}{\cos30^{\circ}}=\frac{\frac{3a}{2}}{\frac{\sqrt{3}}{2}}=a\sqrt{3},
CK=\frac{a\sqrt{3}}{2}=\frac{1}{2}OC=OK,
r=MK=\frac{1}{3}CK=\frac{1}{3}\cdot\frac{1}{2}OC=\frac{1}{3}OK=\frac{1}{3}DO\ctg\angle DKO=\frac{1}{3}d\ctg\alpha.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 9, с. 39

