8201. Пусть ABC
— равносторонний треугольник. Через прямые AB
, BC
и AC
проходят три плоскости, образующие угол \varphi
с плоскостью ABC
и пересекающиеся в точке D_{1}
. Кроме того, через эти же прямые проходят плоскости, образующие угол 2\varphi
с плоскостью ABC
и пересекающиеся в точке D_{2}
. Найдите \varphi
, если известно, что точки D_{1}
и D_{2}
находятся на равных расстояниях от плоскости ABC
.
Ответ. 30^{\circ}
.
Решение. Обозначим через a
сторону равностороннего треугольника ABC
. Тогда радиус вписанной окружности треугольника равен \frac{a\sqrt{3}}{6}
, а радиус вневписанной окружности — \frac{a\sqrt{3}}{2}
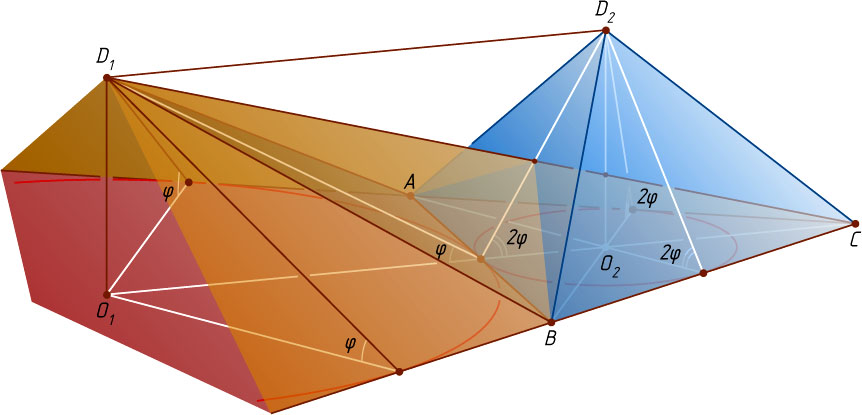
. Боковые грани треугольной пирамиды ABCD_{1}
образуют равные углы с плоскостью основания ABC
, поэтому высота D_{1}O_{1}
пирамиды проходит через центр вписанной или через центр вневписанной окружности треугольника ABC
. Аналогично, высота D_{2}O_{2}
также проходит через центр вписанной или через центр вневписанной окружности треугольника ABC
.
Если O_{1}
и O_{2}
совпадают с центром вписанной окружности треугольника ABC
или и O_{1}
, и O_{2}
являются центрами вневписанных окружностей, то либо
D_{1}O_{1}=\frac{a\sqrt{3}}{6}\cdot\tg\varphi\lt\frac{a\sqrt{3}}{6}\cdot\tg2\varphi=D_{2}O_{2},
либо
D_{1}O_{1}=\frac{a\sqrt{3}}{2}\cdot\tg\varphi\lt\frac{a\sqrt{3}}{2}\cdot\tg2\varphi=D_{2}O_{2},
что противоречит условию задачи (D_{1}O_{1}=D_{2}O_{2}
).
Если O_{1}
— центр вписанной, а O_{2}
— вневписанной окружности треугольника ABC
, то
D_{1}O_{1}=\frac{a\sqrt{3}}{6}\cdot\tg\varphi,~D_{2}O_{2}=\frac{a\sqrt{3}}{2}\cdot\tg2\varphi,
\frac{a\sqrt{3}}{6}\cdot\tg\varphi=\frac{a\sqrt{3}}{2}\cdot\tg2\varphi,
\tg\varphi=3\tg2\varphi,~\tg\varphi=\frac{6\tg\varphi}{1-\tg^{2}\varphi},
откуда \tg^{2}\varphi=-5
, что невозможно.
Если O_{1}
— центр вневписанной, а O_{2}
— вписанной окружности треугольника ABC
, то
D_{1}O_{1}=\frac{a\sqrt{3}}{2}\cdot\tg\varphi,~D_{2}O_{2}=\frac{a\sqrt{3}}{6}\cdot\tg2\varphi,
\frac{a\sqrt{3}}{2}\cdot\tg\varphi=\frac{a\sqrt{3}}{6}\cdot\tg2\varphi,
3\tg\varphi=\tg2\varphi,~3\tg\varphi=\frac{2\tg\varphi}{1-\tg^{2}\varphi},
откуда \tg^{2}\varphi=\frac{1}{3}
, \varphi=30^{\circ}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 10, с. 40
