8202. Отрезки AD
, BD
и CD
попарно перпендикулярны. Известно, что площадь треугольника ABC
равна S
, а площадь треугольника ABD
равна Q
. Найдите площадь ортогональной проекции треугольника ABD
на плоскость ABC
.
Ответ. \frac{Q^{2}}{S}
.
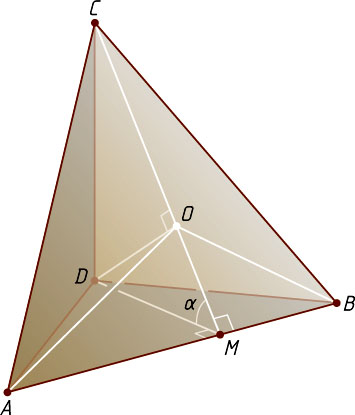
Решение. Пусть O
— ортогональная проекция точки D
на плоскость ABC
. Тогда треугольник AOB
есть ортогональная проекция треугольника ABD
на плоскость ABC
. Пусть прямая CO
пересекает прямую AB
в точке M
. Прямая DC
перпендикулярна двум пересекающимся прямым DA
и DB
плоскости ADB
. Поэтому DC\perp AB
. Таким образом, прямая AB
перпендикулярна двум пересекающимся прямым DC
и DO
плоскости CMD
. Значит, CMD
— линейный угол двугранного угла, образованного плоскостями ABC
и ABD
.
Обозначим \angle CMD=\alpha
. По теореме о площади ортогональной проекции
\cos\alpha=\frac{S_{\triangle ADB}}{S_{\triangle ABC}}=\frac{Q}{S}.
Следовательно,
S_{\triangle AOB}=S_{\triangle ADB}\cos\alpha=Q\cdot\frac{Q}{S}=\frac{Q^{2}}{S}.
