8205. В пирамиде ABCD
двугранные углы с рёбрами AB
, BC
и CA
равны \alpha_{1}
, \alpha_{2}
и \alpha_{3}
соответственно, а площади треугольников ABD
, BCD
и CAD
равны соответственно S_{1}
, S_{2}
и S_{3}
. Площадь треугольника ABC
равна S
. Докажите, что S=S_{1}\cos\alpha_{1}+S_{2}\cos\alpha_{2}+S_{3}\cos\alpha_{3}
(некоторые из углов \alpha_{1}
, \alpha_{2}
и \alpha_{3}
могут быть тупыми).
Решение. Пусть O
— основание высоты DO
пирамиды ABCD
. Тогда треугольники AOB
, AOC
и BOC
— ортогональные проекции треугольников соответственно ADB
, ADC
и BDC
на плоскость ABC
.
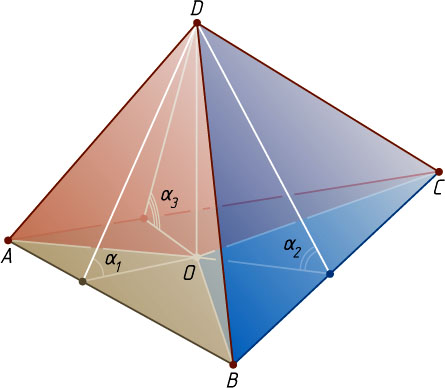
Если основание O
высоты DO
лежит внутри треугольника ABC
(рис. 1), то углы \alpha_{1}
, \alpha_{2}
и \alpha_{3}
— острые, поэтому
S_{\triangle AOB}=S_{\triangle ADB}\cos\alpha_{1}=S_{1}\cos\alpha_{1},
S_{\triangle AOC}=S_{\triangle ADC}\cos\alpha_{2}=S_{2}\cos\alpha_{2},
S_{\triangle BOC}=S_{\triangle BDC}\cos\alpha_{3}=S_{3}\cos\alpha_{3}.
Следовательно,
S=S_{\triangle AOB}+S_{\triangle AOC}+S_{\triangle BOC}=S_{1}\cos\alpha_{1}+S_{2}\cos\alpha_{2}+S_{3}\cos\alpha_{3}.
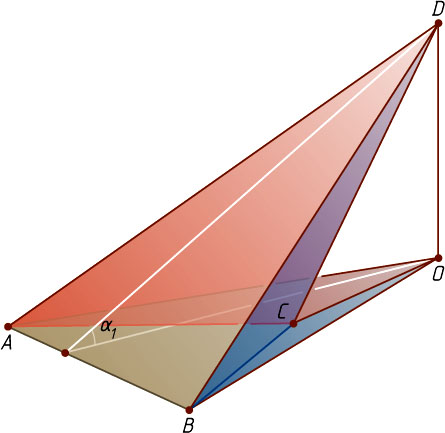
Если основание O
высоты DO
лежит вне треугольника ABC
(рис. 2), то два из углов \alpha_{1}
, \alpha_{2}
и \alpha_{3}
— тупые. Тогда, например, в случае, когда \alpha_{2}\gt90^{\circ}
и \alpha_{3}\gt90^{\circ}
, получим, что
S=S_{\triangle AOB}-S_{\triangle AOC}-S_{\triangle BOC}=
=S_{1}\cos\alpha_{1}-S_{2}\cos(180^{\circ}-\alpha_{2})-S_{3}\cos(180^{\circ}-\alpha_{3})=
=S_{1}\cos\alpha_{1}+S_{2}\cos\alpha_{2}+S_{3}\cos\alpha_{3}.
Аналогично для остальных случаев.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 14, с. 40
Источник: Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии. — М.: Наука, 1989. — № 2.17, с. 32
Источник: Прасолов В. В. Задачи по стереометрии. — 2-е изд. — М.: МЦНМО, 2016. — № 2.18, с. 21

