8206. Из точки M
, расположенной внутри двугранного угла, равного \varphi
, опущены перпендикуляры на его грани (имеются в виду лучи, выходящие из точки M
). Докажите, что угол между этими перпендикулярами равен 180^{\circ}-\varphi
.
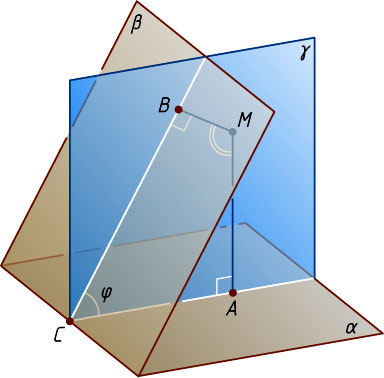
Решение. Пусть указанные перпендикуляры пересекают грани \alpha
и \beta
данного двугранного угла в точках A
и B
. Через пересекающиеся прямые MA
и MB
проведём плоскость \gamma
. Пусть эта плоскость пересекает ребро a
двугранного угла в точке C
. Поскольку прямая a
перпендикулярна двум пересекающимся прямым MA
и MB
плоскости \gamma
, прямая a
перпендикулярна плоскости \gamma
. Значит, ACB
— линейный угол данного двугранного угла. По условию задачи \angle ACB=\varphi
. В плоскости \gamma
из точки M
, лежащей внутри угла ACB
опущены перпендикуляры MA
и MB
на стороны этого угла. Следовательно,
\angle AMB=180^{\circ}-\angle ACB=180^{\circ}-\varphi.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 15, с. 40
