8207. Площадь ортогональной проекции круга радиуса, равного 1, на плоскость \alpha
равна 1. Найдите длину ортогональной проекции этого круга на прямую, перпендикулярную плоскости \alpha
.
Ответ. \frac{2\sqrt{\pi^{2}-1}}{\pi}
.
Решение. Пусть \varphi
— угол между плоскостью \alpha
и плоскостью данного круга, S
— площадь данного круга радиуса r=1
, S_{1}
— площадь его ортогональной проекции на плоскость \alpha
. Тогда по теореме о площади ортогональной проекции
S_{1}=S\cos\varphi,~\mbox{или}~1=\pi r^{2}\cos\varphi=\pi\cos\varphi,
откуда находим, что \cos\varphi=\frac{1}{\pi}
. Тогда
\sin\varphi=\sqrt{1-\cos^{2}\varphi}=\sqrt{1-\frac{1}{\pi^{2}}}=\frac{\sqrt{\pi^{2}-1}}{\pi}.
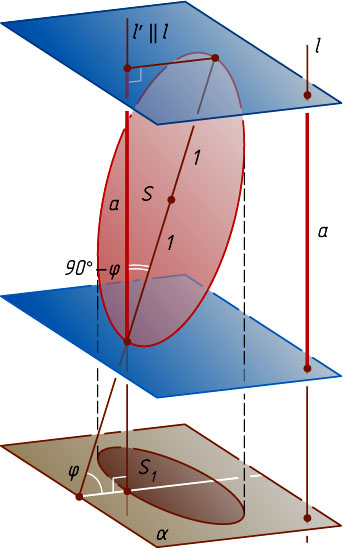
Пусть a
— ортогональная проекция данного круга на прямую l
, перпендикулярную плоскости \alpha
. Тогда
a=2r\cos(90^{\circ}-\varphi)=2r\sin\varphi=\frac{2\sqrt{\pi^{2}-1}}{\pi}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 16, с. 40
