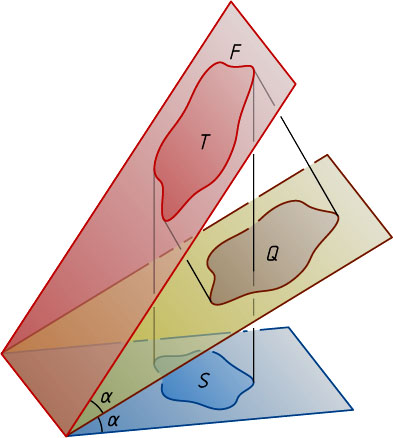
8210. В плоскости одной из граней двугранного угла взята фигура F
. Площадь ортогональной проекции этой фигуры на другую грань равна S
, а площадь её ортогональной проекции на биссекторную плоскость равна Q
. Найдите площадь фигуры F
.
Ответ. \frac{1}{2}(\sqrt{S^{2}+8Q^{2}}-S)
.
Решение. Пусть T
— площадь данной фигуры F
, 2\alpha
— величина данного двугранного угла. По теореме о площади ортогональной проекции
S=T\cos2\alpha,~Q=T\cos\alpha.
Разделив почленно эти равенства, получим, что
\frac{\cos2\alpha}{\cos\alpha}=\frac{S}{Q},~Q(2\cos^{2}\alpha-1)=S\cos\alpha,~2Q\cos^{2}\alpha-S\cos\alpha-Q=0,
\cos\alpha=\frac{S+\sqrt{S^{2}+8Q^{2}}}{4Q}
(так как \alpha\lt90^{\circ}
, то второй корень не подходит). Следовательно,
T=\frac{Q}{\cos\alpha}=\frac{Q}{\frac{S+\sqrt{S^{2}+8Q^{2}}}{4Q}}=\frac{4Q^{2}}{S+\sqrt{S^{2}+8Q^{2}}}=\frac{1}{2}(\sqrt{S^{2}+8Q^{2}}-S).
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 19, с. 41
