8211. Плоские углы при вершине D
пирамиды ABCD
равны 90^{\circ}
. Обозначим через S_{1}
, S_{2}
, S_{3}
и Q
площади граней ABD
, BCD
, CAD
и ABC
соответственно, через \alpha
, \beta
и \gamma
— двугранные углы при рёбрах соответственно AB
, BC
и AC
.
1. Выразите \alpha
, \beta
и \gamma
через S_{1}
, S_{2}
, S_{3}
и Q
.
2. Докажите, что S^{2}_{1}+S^{2}_{2}+S^{2}_{3}=Q^{2}
.
3. Докажите, что \cos^{2}\alpha+\cos^{2}\beta+\cos^{2}\gamma=1
.
Ответ. \cos\alpha=\frac{S_{1}}{Q}
; \cos\beta=\frac{S_{2}}{Q}
; \cos\gamma=\frac{S_{3}}{Q}
.
Решение. Прямая CD
перпендикулярна двум пересекающимся прямым AD
и BD
плоскости ABD
, поэтому прямая CD
перпендикулярна этой плоскости. Значит, треугольник ABD
есть ортогональная проекция треугольника ABC
на плоскость ABD
. По теореме о площади ортогональной проекции S_{\triangle ABD}=S_{\triangle ABC}\cos\alpha
, откуда находим, что
\cos\alpha=\frac{S_{\triangle ABD}}{S_{\triangle ABC}}=\frac{S_{1}}{Q}.
Аналогично, \cos\beta=\frac{S_{2}}{Q}
и \cos\gamma=\frac{S_{3}}{Q}
.
Обозначим AD=a
, BD=b
, CD=c
. Тогда
S_{1}=\frac{1}{2}AD\cdot BD=\frac{1}{2}ab,~S_{2}=\frac{1}{2}BD\cdot CD=\frac{1}{2}bc,~S_{3}=\frac{1}{2}AD\cdot CD=\frac{1}{2}ac.
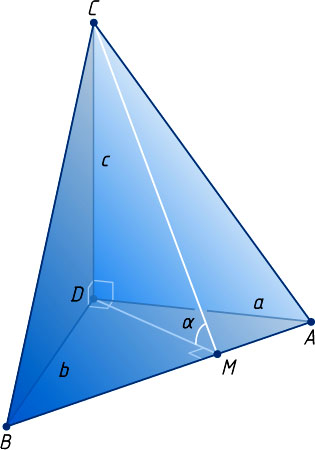
Пусть CM
— высота треугольника ABC
. Тогда по теореме о трёх перпендикулярах DM
— высота прямоугольного треугольника ABD
. Далее имеем:
DM^{2}=\frac{AD^{2}\cdot BD^{2}}{AB^{2}}=\frac{a^{2}b^{2}}{a^{2}+b^{2}},
CM^{2}=DM^{2}+CD^{2}=\frac{a^{2}b^{2}}{a^{2}+b^{2}}+c^{2}=\frac{a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2}}{a^{2}+b^{2}},
S^{2}_{1}+S^{2}_{2}+S^{2}_{3}=\frac{1}{4}a^{2}b^{2}+\frac{1}{4}b^{2}c^{2}+\frac{1}{4}a^{2}c^{2}=
=\frac{1}{4}(a^{2}b^{2}+b^{2}c^{2}+a^{2}c^{2})=\frac{1}{4}CM^{2}(a^{2}+b^{2})=\frac{1}{4}CM^{2}\cdot AB^{2}=Q^{2},
\cos^{2}\alpha+\cos^{2}\beta+\cos^{2}\gamma=\left(\frac{S_{1}}{Q}\right)^{2}+\left(\frac{S_{2}}{Q}\right)^{2}+\left(\frac{S_{3}}{Q}\right)^{2}=
=\frac{S^{2}_{1}+S^{2}_{2}+S^{2}_{3}}{Q^{2}}=\frac{Q^{2}}{Q^{2}}=1.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 20, с. 41