8212. Найдите сторону правильного треугольника, являющегося ортогональной проекцией треугольника со сторонами \sqrt{6}
, 3 и \sqrt{14}
на некоторую плоскость.
Ответ. \sqrt{5}
.
Решение. Пусть треугольник ABC
, в котором AB=\sqrt{14}
, BC=\sqrt{6}
и AC=3
, ортогонально проектируется на плоскость \alpha
и его проекцией является равносторонний треугольник. Будем считать, что вершина A
лежит в плоскости \alpha
. Докажем, что тогда вершины B
и C
должны располагаться по одну сторону от плоскости \alpha
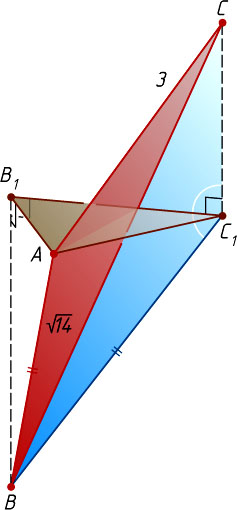
. Предположим, что это не так. Пусть точки B
и C
расположены по разные стороны от плоскости \alpha
(рис. 1), а B_{1}
и C_{1}
— ортогональные проекции этих точек на плоскость \alpha
. Тогда в треугольнике BC_{1}C
угол при вершине C_{1}
— тупой, поэтому BC\gt BC_{1}
. В то же время, BC_{1}=AB
как гипотенузы равных прямоугольных треугольников AB_{1}B
и C_{1}B_{1}B
. Значит, BC\gt AB
, что невозможно, так как AB
— наибольшая сторона треугольника ABC
.
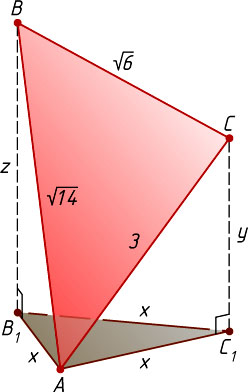
Обозначим AB_{1}=AC_{1}=B_{1}C_{1}=x
, BB_{1}=z
, CC_{1}=y
(рис. 2). Из прямоугольных треугольников AB_{1}B
, AC_{1}C
и из прямоугольной трапеции BB_{1}C_{1}C
находим, что
x^{2}+z^{2}=14,~x^{2}+y^{2}=9,~x^{2}+(z-y)^{2}=6.
Вычитая почленно первое уравнение из второго и третьего, получим систему
\syst{y^{2}-z^{2}=-5\\y^{2}-2yz=-8.\\}
Далее имеем:
z=\frac{y^{2}+8}{2y},~y^{2}-\frac{(y^{2}+8)^{2}}{4y^{2}}+5=0,~4y^{4}-y^{4}-16y^{2}-64+20y^{2}=0,
3y^{4}+4y^{2}-64=0,~y^{2}=4,~x^{2}=9-y^{2}=5.
Следовательно, x=\sqrt{5}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — с. 43
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — Пример 1, с. 6

