8216. Нарисуйте изображение куба, полученное в результате ортогонального проектирования куба на плоскость, перпендикулярную диагонали куба.
Ответ. Правильный шестиугольник со стороной \frac{a\sqrt{2}}{\sqrt{3}}
, где a
— ребро куба.
Указание. Сумма углов, которые произвольная прямая образует с плоскостью и прямой, перпендикулярной этой плоскости, равна 90^{\circ}
.
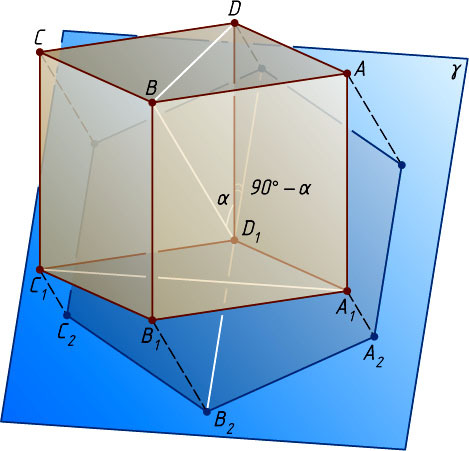
Решение. Рассмотрим ортогональную проекцию куба ABCDA_{1}B_{1}C_{1}D_{1}
(рис. 1) с ребром a
на плоскость \gamma
, перпендикулярную диагонали BD_{1}
и проходящую через вершину D_{1}
. При этом проектировании вершины B
и D_{1}
перейдут в точку D_{1}
.
Пусть \alpha
— угол между ребром DD_{1}
и диагональю BD_{1}
(рис. 2). Тогда угол между прямой DD_{1}
и плоскостью \gamma
равен 90^{\circ}-\alpha
. Из прямоугольного треугольника BDD_{1}
находим, что
\cos\alpha=\frac{DD_{1}}{BD_{1}}=\frac{a}{a\sqrt{3}}=\frac{1}{\sqrt{3}},~\sin\alpha=\frac{BD}{BD_{1}}=\frac{a\sqrt{2}}{a\sqrt{3}}=\frac{\sqrt{2}}{\sqrt{3}}.
Значит, ортогональная проекция ребра DD_{1}
на плоскость \gamma
равна
DD_{1}\cos(90^{\circ}-\alpha)=a\sin\alpha=\frac{a\sqrt{2}}{\sqrt{3}}.
Поскольку рёбра AA_{1}
, CC_{1}
и BB_{1}
равны и параллельны ребру DD_{1}
, их ортогональные проекции на плоскость \gamma
также равны \frac{a\sqrt{2}}{\sqrt{3}}
.
Ясно, что угол между ребром C_{1}D_{1}
и диагональю BD_{1}
также равен \alpha
. Значит, ортогональная проекция ребра C_{1}D_{1}
на плоскость \gamma
равна C_{1}D_{1}\cos(90^{\circ}-\alpha)=a\sin\alpha=\frac{a\sqrt{2}}{\sqrt{3}}
.
Поскольку рёбра AB
, A_{1}B_{1}
и CD
равны и параллельны ребру C_{1}D_{1}
, их ортогональные проекции на плоскость \gamma
также равны \frac{a\sqrt{2}}{\sqrt{3}}
.
Таким образом, ортогональная проекция куба на плоскость \gamma
есть шестиугольник, все стороны которого равны \frac{a\sqrt{2}}{\sqrt{3}}
. Так как диагональ AC
квадрата ABCD
перпендикулярна диагонали BD_{1}
куба, то её ортогональная проекция на плоскость \gamma
параллельна и равна отрезку AC=a\sqrt{2}
.
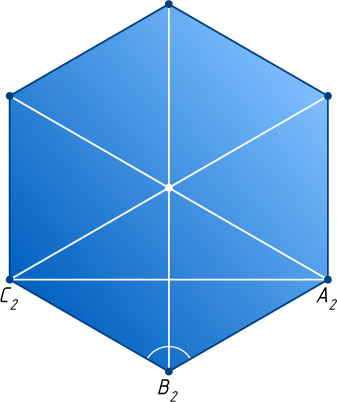
Пусть A_{2}
, B_{2}
и C_{2}
— ортогональные проекции вершин соответственно A
, B
и C
на плоскость \gamma
(рис. 3). Тогда в треугольнике A_{2}B_{2}C_{2}
известно, что
A_{2}C_{2}=a\sqrt{2},~A_{2}B_{2}=B_{2}C_{2}=\frac{a\sqrt{2}}{\sqrt{3}}.
Поэтому \angle A_{2}B_{2}C_{2}=120^{\circ}
. Аналогично, все углы шестиугольника, являющегося ортогональной проекцией куба ABCDA_{1}B_{1}C_{1}D_{1}
на плоскость \gamma
, равны 120^{\circ}
. Следовательно, этот шестиугольник правильный.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 5(а,в), с. 46

