8217. На плоскости отмечены три точки, служащие изображениями (параллельными проекциями) трёх последовательных вершин правильного шестиугольника. Постройте изображения остальных вершин шестиугольника.
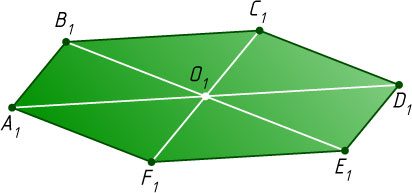
Решение. При параллельном проектировании равные и параллельные отрезки переходят в равные и параллельные между собой отрезки. Пусть A_{1}
, B_{1}
и C_{1}
— данные изображения последовательных вершин соответственно A
, B
и C
правильного шестиугольника ABCDEF
с центром O
. Известно, что
AB\parallel OC\parallel OF\parallel DE,~AB=OC=OF=DE.
Значит, ABOF
, ABCO
, OCDE
и ODEF
— параллелограммы. Пусть C_{1}
, D_{1}
, E_{1}
, F_{1}
и O_{1}
— изображения точек C
, D
, E
, F
и O
соответственно. Тогда A_{1}B_{1}O_{1}F_{1}
, A_{1}B_{1}C_{1}O_{1}
, O_{1}C_{1}D_{1}E_{1}
и O_{1}D_{1}E_{1}F_{1}
— также параллелограммы. Отсюда вытекает нужное построение.
