8218. Дано изображение (параллельная проекция на некоторую плоскость) треугольника и центра описанной около него окружности. Постройте изображение точки пересечения высот этого треугольника.
Указание. Высота PP_{1}
треугольника PQR
параллельна серединному перпендикуляру отрезка QR
.
Решение. При параллельном проектировании сохраняется отношение отрезков, лежащих на одной прямой или на параллельных прямых. Поэтому изображениями середин M
и N
сторон AB
и AC
треугольника ABC
являются середины M_{1}
и N_{1}
сторон A_{1}B_{1}
и A_{1}C_{1}
треугольника A_{1}B_{1}C_{1}
— изображения треугольника ABC
.
Пусть H
— точка пересечения высот треугольника ABC
. Тогда CH\parallel OM
и BH\parallel ON
, где O
— центр описанной окружности треугольника ABC
. При параллельном проектирование сохраняется параллельность прямых. Поэтому C_{1}H_{1}\parallel O_{1}M_{1}
и B_{1}H_{1}\parallel O_{1}N_{1}
, где O_{1}
— изображение точки O
. Отсюда вытекает следующее построение.
Строим середины M_{1}
и N_{1}
данных сторон A_{1}B_{1}
и A_{1}C_{1}
. Через точки C_{1}
и B_{1}
проводим прямые, параллельные O_{1}M_{1}
и O_{1}N_{1}
соответственно. Точка H_{1}
пересечения построенных прямых есть искомое изображение точки пересечения высот треугольника ABC
.
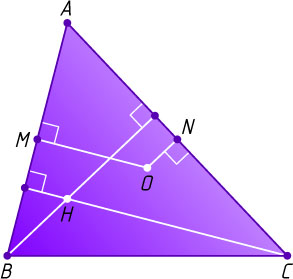
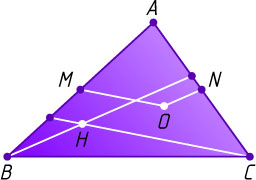
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 10, с. 47

