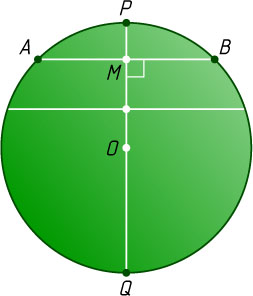
8219. На плоскости нарисована линия, являющаяся изображением (параллельной проекцией на некоторую плоскость) окружности. Постройте изображение центра этой окружности.
Решение. Пусть A_{1}B_{1}
— изображение хорды AB
окружности, M
— середина AB
. Поскольку при параллельном проектировании середина отрезка переходит в середину проекции этого отрезка, то изображение M_{1}
точки M
есть середина A_{1}B_{1}
.
Известно, что прямая, проходящая через середины двух параллельных хорд окружности, проходит через центр окружности. Кроме того, при параллельном проектировании сохраняется параллельность прямых. Отсюда вытекает следующее построение.
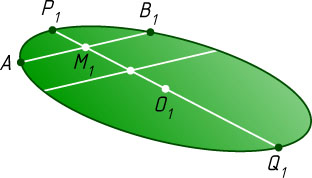
Строим два параллельных отрезка с концами на данном изображении окружности. Затем проводим прямую через середины этих отрезков. Таким образом, мы построили изображение P_{1}Q_{1}
какого-то диаметра PQ
окружности. Середина O_{1}
отрезка P_{1}Q_{1}
есть изображение центра окружности.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 11, с. 47

