8220. На плоскости даны изображение (параллельная проекция) плоского четырёхугольника ABCD
и точки M
, не лежащей в его плоскости. Постройте изображение прямой, по которой пересекаются плоскости ABM
и CDM
.
Решение. Пусть A_{1}
, B_{1}
, C_{1}
, D_{1}
— изображения вершин соответственно A
, B
, C
, D
четырёхугольника ABCD
, M_{1}
— изображение точки M
. Если прямые AB
и CD
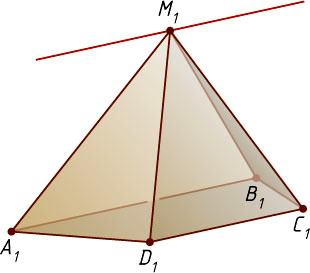
параллельны (рис. 1), то по теореме о пересекающихся плоскостях, проходящих через две параллельные прямые, прямая пересечения плоскостей ABM
и CDM
параллельна каждой из прямых AB
и CD
. При параллельном проектировании сохраняется параллельность прямых. Значит, изображение прямой пересечения плоскостей ABM
и CDM
есть прямая, проходящая через точку M_{1}
параллельно A_{1}B_{1}
и C_{1}D_{1}
.
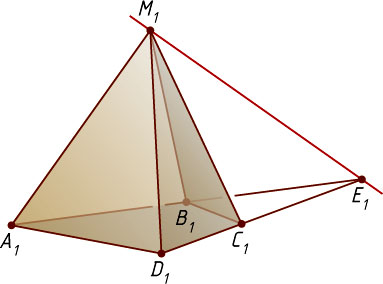
Если прямые AB
и CD
пересекаются в точке E
, изображение E_{1}
точки E
есть точка пересечения прямых A_{1}B_{1}
и C_{1}D_{1}
(рис. 2). В этом случае изображением прямой пересечения плоскостей ABM
и CDM
является прямая M_{1}E_{1}
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 12, с. 47

