8221. Площадь треугольника ABC
равна 2. Найдите площадь сечения пирамиды ABCD
плоскостью, проходящей через середины рёбер AD
, BD
, CD
.
Ответ. \frac{1}{2}
.
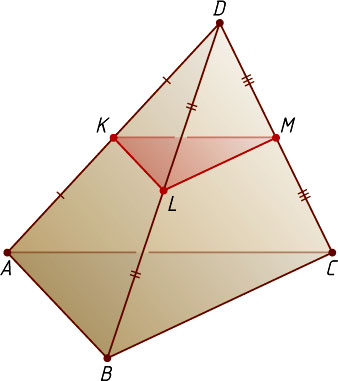
Решение. В сечении получится треугольник KLM
, стороны которого — средние линии треугольников ADB
, BDC
и ADC
. Значит, треугольник KLM
подобен треугольнику ABC
с коэффициентом \frac{1}{2}
. Следовательно, площадь треугольника KLM
равна площади треугольника ABC
, умноженной на квадрат коэффициента подобия, т. е.
S_{\triangle KLM}=\left(\frac{1}{2}\right)^{2}\cdot S_{\triangle ABC}=\frac{1}{4}\cdot2=\frac{1}{2}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 2, с. 52
