8223. Докажите, что сечением пирамиды ABCD
плоскостью, параллельной рёбрам AC
и BD
, является параллелограмм, причём для одной такой плоскости этот параллелограмм будет ромбом. Найдите сторону этого ромба, если AC=a
, BD=b
.
Ответ. \frac{ab}{a+b}
.
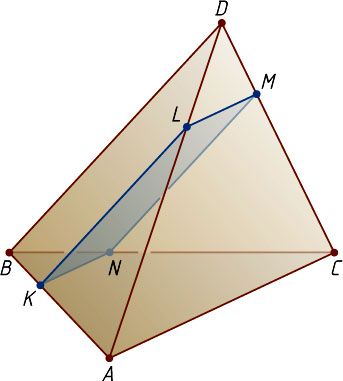
Решение. Пусть секущая плоскость пересекает рёбра AB
, AD
, CD
и BC
в точках K
, L
, M
и N
соответственно. Плоскость ABD
проходит через прямую BD
, параллельную секущей плоскости, и пересекает секущую плоскость по прямой KL
. Значит, KL\parallel BD
. Аналогично, MN\parallel BD
. Поэтому KL\parallel MN
. Аналогично, что KN\parallel LM
. Следовательно, KLMN
— параллелограмм.
Обозначим \frac{DL}{DA}=\frac{DM}{DC}=k
. Тогда \frac{AL}{AD}=\frac{AK}{AB}=1-k
. Поэтому
LM=kAC=ka,~KL=(1-k)BD=(1-k)b.
Параллелограмм KLMN
является ромбом, если LM=KL
. Из уравнения ka=(1-k)b
находим, что k=\frac{b}{a+b}
. Следовательно,
KL=LM=ka=\frac{ab}{a+b}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 4, с. 53
