8224. На рёбрах AB
, BC
и BD
пирамиды ABCD
взяты точки K
, L
и M
соответственно. Постройте прямую пересечения плоскостей CDK
и MLA
.
Решение. Пусть прямые CK
и AL
пересекаются в точке N
. Тогда точка N
лежит в плоскости CDK
и в плоскости MLA
. Значит, точка N
принадлежит прямой пересечения плоскостей CDK
и MLA
.
Пусть прямые DK
и AM
пересекаются в точке P
. Тогда точка P
лежит в плоскости CDK
и в плоскости MLA
. Значит, точка P
принадлежит прямой пересечения плоскостей CDK
и MLA
.
Таким образом, точки P
и N
принадлежат прямой пересечения плоскостей CDK
и MLA
. Следовательно, PN
— искомая прямая, по которой пересекаются плоскости CDK
и MLA
.
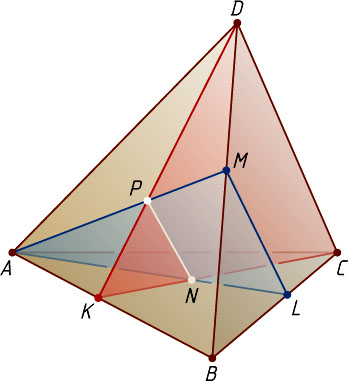
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 6(а), с. 53
