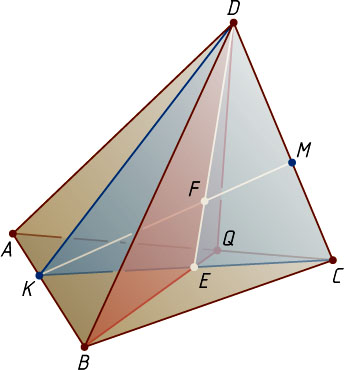
8227. На рёбрах AB
, CD
и AC
пирамиды ABCD
взяты точки K
, M
и Q
соответственно. Постройте точку пересечения прямой KM
с плоскостью BDQ
.
Решение. Пусть E
— точка пересечения прямых CK
и BQ
. Тогда D
и E
— общие точки плоскостей BDQ
и CDK
. Значит, плоскости BDQ
и CDK
пересекаются по прямой DE
. Прямые KM
и DE
, лежащие в плоскости CDK
, пересекаются в точке F
. Следовательно, F
— точка пересечения прямой KM
с плоскостью BDQ
.