8228. На рёбрах AD
, DC
и BC
пирамиды ABCD
взяты точки K
, L
и M
соответственно. Постройте прямую, проходящую через точку M
и пересекающую прямые BK
и AL
.
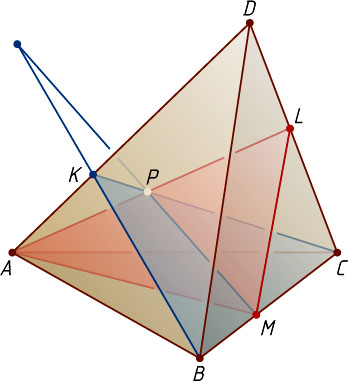
Решение. Пусть прямые AL
и CK
пересекаются в точке P
. Тогда P
и M
— общие точки плоскостей BKC
и AML
. Значит, плоскости BKC
и AML
пересекаются по прямой MP
. Прямая MP
пересекает прямую AL
. Если прямая MP
пересекает лежащую с ней в одной плоскости (BKC
) прямую BK
, то прямая MP
— искомая. Если MP\parallel BK
, то задача не имеет решений.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. —
