8229. На рёбрах AB
, BC
, CD
, DA
, BD
и AC
пирамиды ABCD
взяты точки K
, L
, M
, P
, N
и Q
соответственно. Постройте прямую, по которой пересекаются плоскости KLM
и PNQ
.
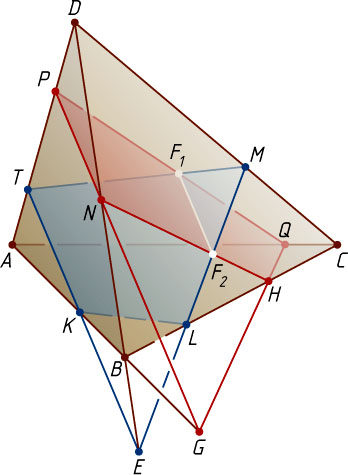
Решение. Предположим, что прямые ML
и BD
пересекаются в точке E
, прямые EK
и AD
— в точке T
, прямые TM
и PQ
— в точке F_{1}
. Тогда F_{1}
— общая точка плоскостей KLM
и PNQ
.
Предположим, что прямые PN
и AB
пересекаются в точке G
, прямые GQ
и BC
— в точке H
, а прямые NH
и ML
— в точке F_{2}
. Тогда F_{2}
— также общая точка плоскостей KLM
и PNQ
. Следовательно, F_{1}F_{2}
— искомая прямая.
