8230. На рёбрах AB
, BC
, CD
, DA
, BD
и AC
пирамиды ABCD
взяты точки K
, L
, M
, P
, N
и Q
соответственно. Постройте точку пересечения плоскостей ALM
, CNP
и DKQ
.
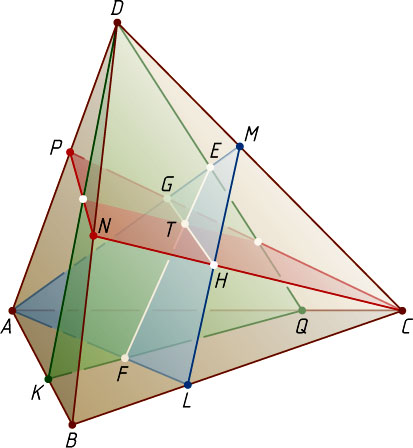
Решение. Пусть G
— точка пересечения прямых AM
и CP
, H
— точка пересечения прямых CN
и ML
. Тогда GH
— прямая пересечения плоскостей ALM
и CNP
.
Пусть E
— точка пересечения прямых AM
и DQ
, F
— точка пересечения прямых AL
и KQ
. Тогда EF
— прямая пересечения плоскостей ALM
и DKQ
.
Пусть прямые, GH
и EF
, лежащие в плоскости AML
пересекаются в точке T
. Тогда T
— общая точка плоскостей ALM
, CNP
и DKQ
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 7(б), с. 53
