8231. Точка K
лежит на ребре AB
пирамиды ABCD
. Постройте сечение пирамиды плоскостью, проходящей через точку K
параллельно прямым BC
и AD
.
Решение. Плоскость ABD
проходит через прямую AD
, параллельную секущей плоскости, и имеет с секущей плоскостью общую точку K
. Значит, плоскость ABD
и секущая плоскость пересекаются по прямой, проходящей через точку K
параллельно AD
.
Аналогично, секущая плоскость пересекается с плоскостями ABC
и BDC
по прямым, параллельным BC
, а с плоскостью ADC
— по прямой, параллельной AD
.
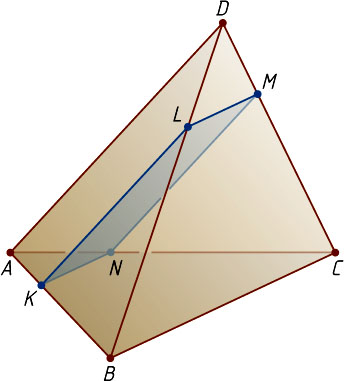
Пусть L
, M
и N
— точки пересечения секущей плоскости с рёбрами BD
, CD
и AC
соответственно. Тогда искомое сечение — параллелограмм KLMN
.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 8, с. 53
