8233. Постройте сечение треугольной пирамиды плоскостью, проходящей через три точки, лежащие в трёх гранях пирамиды.
Решение. Пусть точки K
, L
и M
лежат в гранях соответственно ABD
, BCD
и ACD
треугольной пирамиды ABCD
. Продолжим отрезки DK
, DL
и DM
до пересечения с рёбрами AB
, BC
и AC
соответственно в точках K_{1}
, L_{1}
и M_{1}
. Прямые MK
и M_{1}K_{1}
лежат в плоскости DK_{1}M_{1}
, прямые ML
и M_{1}L_{1}
— в плоскости DM_{1}L_{1}
, прямые KL
и K_{1}L_{1}
— в плоскости DK_{1}L_{1}
.
Если две рассматриваемые пары прямых состоят из параллельных прямых, то прямые третьей пары также параллельны. Если, например, MK\parallel M_{1}K_{1}
и ML\parallel M_{1}L_{1}
, то по признаку параллельности плоскостей секущая плоскость параллельна плоскости ABC
. В этом случае секущая плоскость пересекает плоскости граней ABD
, BCD
и ACD
по прямым, проходящим через точки K
, L
и M
параллельно прямым соответственно AB
, BC
и AC
.
Остался случай, когда две рассматриваемые пары прямых состоят из пересекающихся прямых. Пусть, например, прямые MK
и M_{1}K_{1}
пересекаются в точке P
, а прямые ML
и M_{1}L_{1}
— в точке Q
. Тогда секущая плоскость пересекается с плоскостью ABC
по прямой PQ
. Точки, в которых прямая PQ
пересекает прямые AB
, BC
и AC
принадлежат секущей плоскости. Дальнейшее построение очевидно.
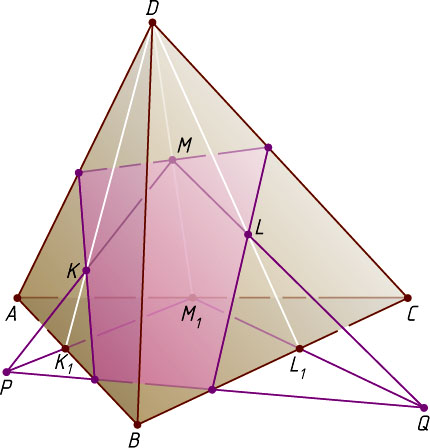
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 10, с. 53
